Fundamental Theorem of Calculus

The definite integral of a function f(x) over the interval [a, b] is equal to the difference between the values of an antiderivative F(x) evaluated at the endpoints: $$ \int_a^b f(x) \:\:dx = F(b) - F(a) $$

What is an antiderivative?

An antiderivative F(x) is a function whose derivative is equal to the original integrand f(x).

Note: Finding an antiderivative for a given function f(x) is not always straightforward. However, when it is possible, computing the definite integral becomes much more efficient.

A Practical Example

Let’s evaluate the following integral:

$$ \int_2^6 3x^2 \:\: dx $$

An antiderivative of f(x) = 3x² is:

$$ F(x) = x^3 $$

because its derivative is equal to f(x):

$$ D[x^3] = 3x^2 $$

Therefore, the definite integral of f(x) from 2 to 6 is:

$$ \int_2^6 3x^2 \:\: dx = F(6) - F(2) = 6^3 - 2^3 = 208 $$

This represents the area under the curve of the function between x = 2 and x = 6.

Proof

Let F(x) and G(x) be two antiderivatives of a continuous function f(t) on the interval [a, x].

$$ G(x) = \int_a^x f(t) \: dt $$

$$ F(x) = \int_a^x f(t) \: dt $$

According to a fundamental property of antiderivatives, any two antiderivatives of the same function differ by a constant:

$$ G(x) - F(x) = k $$

which can be written as:

$$ G(x) = F(x) + k $$

Thus, we can express G(x) as:

$$ G(x) = k + \int_a^x f(t) \: dt $$

Let’s now evaluate the expression at x = a:

$$ G(a) = k + \int_a^a f(t) \: dt $$

$$ G(a) = k + 0 = k $$

Substituting k = G(a), we rewrite the equation as:

$$ G(x) = G(a) + \int_a^x f(t) \: dt $$

Setting x = b gives:

$$ G(b) = G(a) + \int_a^b f(t) \: dt $$

Rearranging terms yields the key identity:

$$ G(b) - G(a) = \int_a^b f(t) \: dt $$

This establishes the Fundamental Theorem of Calculus.

Additional Examples

Example 1

The simplest case of a definite integral is the integral of a constant function:

$$ f(x) = k $$

Over the interval [a, b], its definite integral is:

$$ \int_a^b f(x) \:\: dx = k \cdot (b - a) $$

For instance, if the constant value is 5:

$$ f(x) = 5 $$

Then the integral over [2, 7] is:

$$ \int_2^7 5 \:\: dx = 5 \cdot (7 - 2) = 25 $$

Here is the graphical representation:

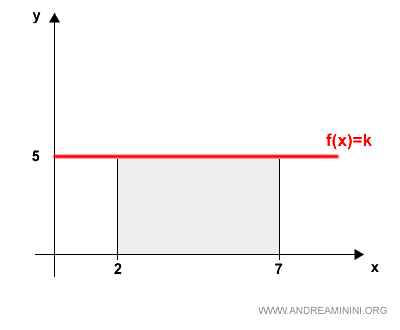
Note: The upper limit of integration (b) does not need to be greater than the lower limit (a). If b < a, the result of the integral is negative: $$ \int_7^2 5 \:\: dx = 5 \cdot (2 - 7) = -25 $$ If the limits are equal (a = b), the integral evaluates to zero: $$ \int_2^2 5 \:\: dx = 5 \cdot (2 - 2) = 0 $$

And so on.