Multiplying a Definite Integral by a Constant

Multiplying the definite integral of a function $ f(x) $ over an interval [a, b] by a constant $ k $ is equivalent to integrating the product $ k \cdot f(x) $ over the same interval:
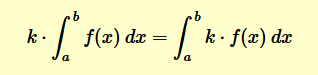
multiplying a definite integral by a constant

This property of definite integrals is especially useful when simplifying expressions during integration.

A Practical Example
Proof

A Practical Example

Let’s consider the definite integral of the function $ f(x) = 2x $ over the interval [2, 5]:

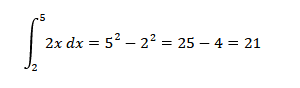
example: integral of f(x) = 2x from 2 to 5

Now let’s compute the integral of the same function multiplied by a constant $ k = 2 $:

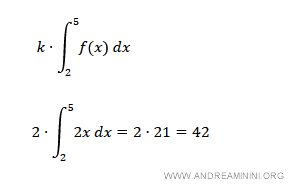
integral of the function times k = 2

Alternatively, we can compute the integral of the function $ k \cdot f(x) $ directly over the interval [2, 5]:

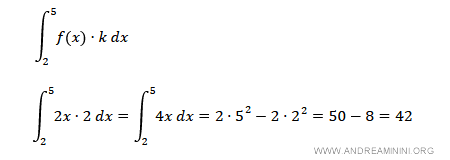
integral of the scaled function over the same interval

As expected, both approaches yield the same result.

Proof

If the function $ f(x) $ is Riemann integrable on the interval [a, b], then for any $ \epsilon > 0 $, there exists a partition $ P $ such that the difference between the upper and lower Darboux sums is less than $ \epsilon / 2 $:

Now consider the function $ k \cdot f(x) $, where $ k \geq 1 $:

The corresponding lower and upper Darboux sums satisfy:

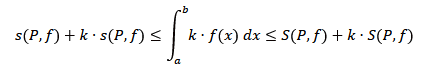
scaled lower and upper Darboux sums

We now need to show that the following inequality holds:

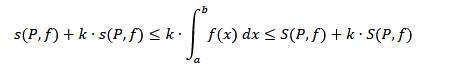
inequality involving k times the integral

To do so, we examine the difference between the two sides:

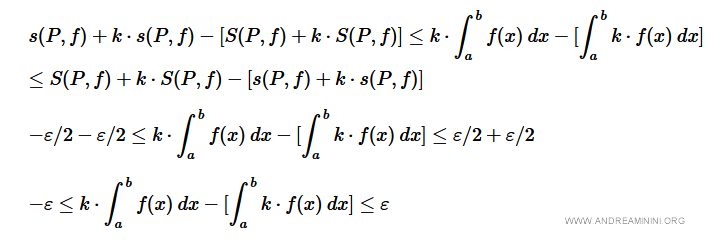
bounded difference between k times the integral and the integral of k times f(x)

This proves that for any arbitrary $ \epsilon > 0 $, the inequality is satisfied, confirming that: $$ k \cdot \int_a^b f(x)\, dx = \int_a^b k \cdot f(x)\, dx $$

And so on.