Integrability Theorem for Continuous Functions

If a function $ f(x) $ is continuous over the interval [a, b], then it is Riemann integrable on [a, b].

Proof

According to the Cantor theorem, any function that is bounded on a closed interval [a, b] is uniformly continuous.

As a consequence, it is also continuous on that interval.

Given any $ \epsilon > 0 $, uniform continuity guarantees the existence of a $ \delta > 0 $ such that:

$$ |f(x) - f(x')| < \frac{\epsilon}{b - a} $$

for all $ x, x' \in [a, b] $ satisfying:

$$ |x - x'| < \delta $$

Now consider an arbitrary partition $ P $ of the interval [a, b]:

$$ P = ( x_0, x_1, x_2, \ldots, x_{n-1}, x_n ) $$

where $ x_0 = a $ and $ x_n = b $, so the partition becomes:

$$ P = ( a, x_1, x_2, \ldots, x_{n-1}, b ) $$

By assumption, the length of each subinterval is smaller than $ \delta $:

$$ |x_k - x_{k-1}| < \delta $$

On each subinterval $[x_{k-1}, x_k]$, define:

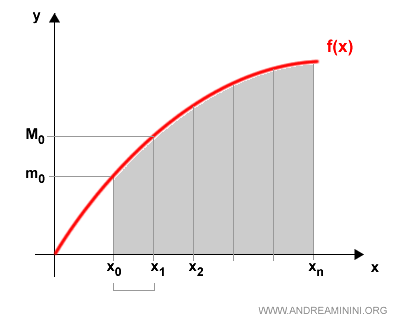
area under the function

$$ m_k = \inf \{ f(x) \mid x \in [x_{k-1}, x_k] \} $$

$$ M_k = \sup \{ f(x) \mid x \in [x_{k-1}, x_k] \} $$

The inequality:

$$ |f(x) - f(x')| < \frac{\epsilon}{b - a} $$

then implies the following bound on the oscillation of $ f $ over each subinterval:

$$ M_k - m_k < \frac{\epsilon}{b - a} $$

Note: The absolute value is not needed here, since by definition the supremum $ M_k $ is greater than or equal to the infimum $ m_k $, so $ M_k - m_k \ge 0 $.

Multiplying both sides by the length of the interval $ x_k - x_{k-1} $, we get:

$$ (M_k - m_k) \cdot (x_k - x_{k-1}) < \frac{\epsilon}{b - a} \cdot (x_k - x_{k-1}) $$

Geometrically, the left-hand side represents the difference between the areas of two rectangles: one with height $ M_k $ and the other with height $ m_k $.

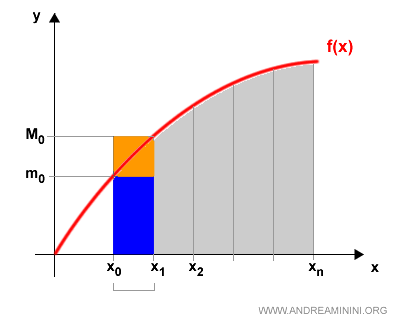
area of the first subinterval

Summing over all subintervals in the partition $ P $, we obtain:

$$ \sum_{k=1}^n (M_k - m_k) \cdot (x_k - x_{k-1}) < \frac{\epsilon}{b - a} \cdot \sum_{k=1}^n (x_k - x_{k-1}) $$

The left-hand side is the difference between the upper and lower Riemann sums:

$$ S(P) - s(P) < \frac{\epsilon}{b - a} \cdot \sum_{k=1}^n (x_k - x_{k-1}) $$

Visually:

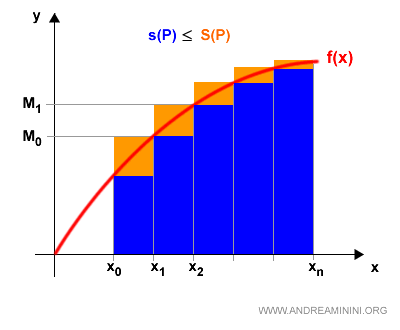
difference between upper and lower Riemann sums

The sum $ \sum_{k=1}^n (x_k - x_{k-1}) $ equals the length of the entire interval:

$$ S(P) - s(P) < \frac{\epsilon}{b - a} \cdot (b - a) $$

Which simplifies to the classic Riemann integrability condition:

$$ S(P) - s(P) < \epsilon $$

This proves that any function continuous on [a, b] is Riemann integrable.

And so on.