Mean Value Theorem for Definite Integrals

If $ f(x) $ is continuous over the interval [a, b], then there exists a point $ x_0 \in [a, b] $ such that $$ \int_a^b f(x) \: dx = f(x_0) \cdot (b - a) $$ 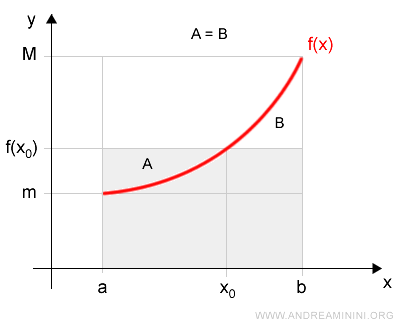areas A and B determined by the mean value x0 are equal

What does this mean?

The area of the rectangle given by $ f(x_0) \cdot (b - a) $ is equal to the area under the curve of $ f(x) $ over the interval [a, b], because the regions A and B have the same area.

areas A and B are equal in value

This means that if we know the value $ x_0 $ where the function reaches its average height on [a, b], we can compute the same result as the definite integral using the expression $ f(x_0) \cdot (b - a) $.

the definite integral of the function over [a, b], represented by the area under the curve

Proof

The definite integral lies between the lower and upper Riemann sums, $ s(P) $ and $ S(P) $, for any partition $ P $ of the interval [a, b]:

$$ s(P) \le \int_a^b f(x) \: dx \le S(P) $$

Let’s consider a simple partition $ P $ made up of just two points: [a, b].

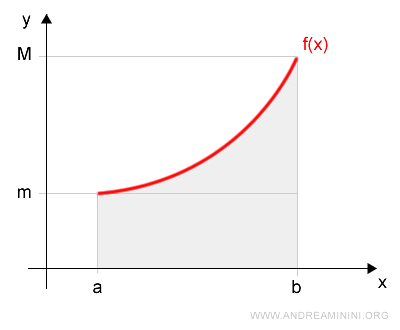
example of a basic partition of the interval

The lower sum, using $ m = \min f(x) $ on [a, b], is:

$$ s(P) = m \cdot (b - a) $$

The upper sum, using $ M = \max f(x) $ on [a, b], is:

$$ S(P) = M \cdot (b - a) $$

Substituting into the inequality gives:

$$ m \cdot (b - a) \le \int_a^b f(x) \: dx \le M \cdot (b - a) $$

Now divide each part of the inequality by $ (b - a) $:

$$ \frac{m \cdot (b - a)}{b - a} \le \frac{1}{b - a} \int_a^b f(x) \: dx \le \frac{M \cdot (b - a)}{b - a} $$

Which simplifies to:

$$ m \le \frac{1}{b - a} \int_a^b f(x) \: dx \le M $$

So there exists a number $ y_0 $ such that:

$$ y_0 = \frac{1}{b - a} \int_a^b f(x) \: dx $$

and:

$$ m \le y_0 \le M $$

By the Intermediate Value Theorem, there must exist a point $ x_0 \in [a, b] $ such that:

$$ y_0 = f(x_0) $$

This confirms the theorem:

$$ \frac{1}{b - a} \int_a^b f(x) \: dx = f(x_0) $$

and thus:

$$ \int_a^b f(x) \: dx = f(x_0) \cdot (b - a) $$

The rectangle formed by $ f(x_0) \cdot (b - a) $ has the same area as the region under the curve of $ f(x) $ over [a, b].

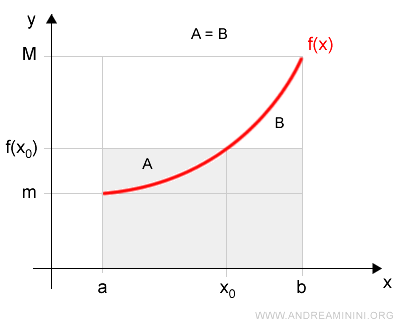
areas A and B determined by the mean value x0 are equal

Therefore, the area given by $ f(x_0) \cdot (b - a) $ exactly matches the definite integral $ \int_a^b f(x) \: dx $.

example of a basic partition of the interval

And so on.