Union of Partitions in an Integral

Given two partitions P and Q of the interval [a, b], the partition R obtained by merging them, $$ R = P \cup Q $$, satisfies the following inequalities: $$ s(P) \le s(R) \le S(R) \le S(Q) $$ Here, \( s() \) denotes the lower Darboux sum and \( S() \) the upper Darboux sum.

The integral sum represents the area of a step-shaped region either inscribed in or circumscribed around the graph of the function, based on the chosen partition.

Proof

Partition P consists of two consecutive points: x_k-1 and x_k.

Partition Q contains three points - one additional point, x, compared to P.

The union of the two partitions, denoted R, therefore consists of three points:

$$ R = P \cup Q = \{ x_{k-1}, x, x_k \} $$

This gives rise to two subintervals: [x_k-1, x] and [x, x_k].

We now compute the lower and upper Darboux sums to establish the order of inequalities.

1] Lower Darboux Sums

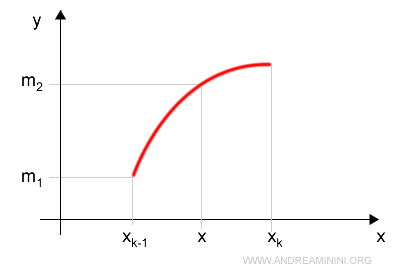
We identify the infimum of the function on each subinterval of R:

$$ m_1 = \inf([x_{k-1}, x]) $$

$$ m_2 = \inf([x, x_k]) $$

Graphically, this looks like:

The lower sums for partitions P and R are given by:

$$ s(P) = m_k \cdot (x_k - x_{k-1}) $$

$$ s(R) = m_1 \cdot (x - x_{k-1}) + m_2 \cdot (x_k - x) $$

Here’s how this is represented graphically:

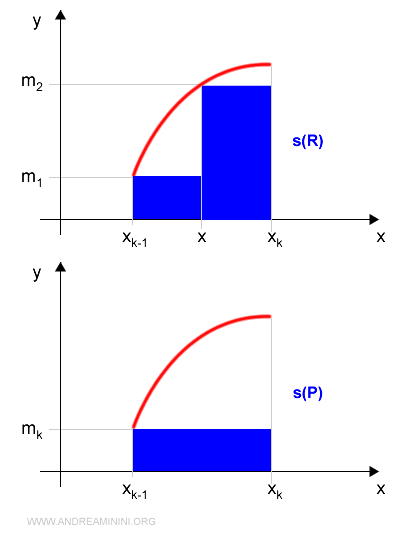
The difference between the two sums is:

$$ s(R) - s(P) = [m_1 \cdot (x - x_{k-1}) + m_2 \cdot (x_k - x)] - m_k \cdot (x_k - x_{k-1}) $$

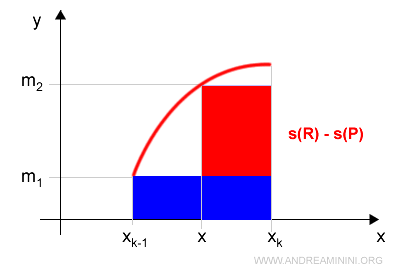
Note: From a geometric standpoint, it's already evident that \( s(R) - s(P) > 0 \). Hence, $$ s(R) \ge s(P) $$

Since

$$ m_1 \ge m_k \quad \text{and} \quad m_2 \ge m_k $$

because the interval [x_k-1, x_k] contains both subintervals [x_k-1, x] and [x, x_k],

we can substitute \( m_k \) in place of \( m_1 \) and \( m_2 \) to obtain:

$$ s(R) - s(P) \ge [m_k \cdot (x - x_{k-1}) + m_k \cdot (x_k - x)] - m_k \cdot (x_k - x_{k-1}) $$

$$ s(R) - s(P) \ge m_k \cdot (x - x_{k-1} + x_k - x - x_k + x_{k-1}) $$

$$ s(R) - s(P) \ge m_k \cdot 0 = 0 $$

Thus, $$ s(R) \ge s(P) $$

2] Upper Darboux Sums

Now, let’s calculate the supremum on each subinterval of R:

$$ M_1 = \sup([x_{k-1}, x]) $$

$$ M_2 = \sup([x, x_k]) $$

Graphically:

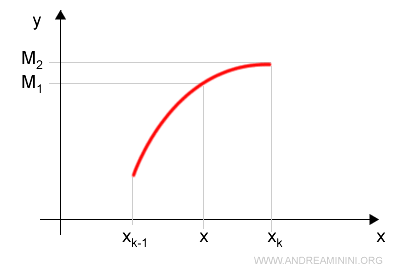
The upper sums for partitions Q and R are:

$$ S(Q) = M_k \cdot (x_k - x_{k-1}) $$

$$ S(R) = M_1 \cdot (x - x_{k-1}) + M_2 \cdot (x_k - x) $$

And here’s the corresponding visual:

The difference between the upper sums is:

$$ S(Q) - S(R) = M_k \cdot (x_k - x_{k-1}) - [M_1 \cdot (x - x_{k-1}) + M_2 \cdot (x_k - x)] $$

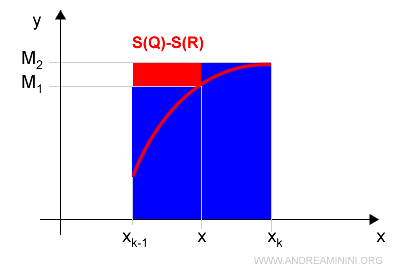
Note: Visually, it's clear that \( S(Q) - S(R) > 0 \), and so we conclude: $$ S(Q) \ge S(R) $$

Since

$$ M_1 \le M_k \quad \text{and} \quad M_2 \le M_k $$

we can again substitute \( M_k \) for both \( M_1 \) and \( M_2 \):

$$ S(Q) - S(R) \ge M_k \cdot (x_k - x_{k-1}) - [M_k \cdot (x - x_{k-1}) + M_k \cdot (x_k - x)] $$

$$ S(Q) - S(R) \ge M_k \cdot (x_k - x_{k-1} - x + x_{k-1} - x_k + x) $$

$$ S(Q) - S(R) \ge M_k \cdot 0 = 0 $$

Thus, $$ S(Q) \ge S(R) $$

3] Final Conclusion

From the analysis of both lower and upper Darboux sums, we’ve established:

$$ s(R) \ge s(P) \quad \text{and} \quad S(Q) \ge S(R) $$

And since upper sums are always at least as large as lower sums, we can consolidate all the inequalities:

$$ S(Q) \ge S(R) \ge s(R) \ge s(P) $$

Or, equivalently:

$$ s(P) \le s(R) \le S(R) \le S(Q) $$

This confirms the initial proposition.

And so on.