Improper Integrals

Improper integrals are definite integrals where either the interval of integration is unbounded, or the integrand becomes unbounded within a finite interval.

Typically, definite integrals are used to evaluate functions that are continuous and bounded over a closed, finite interval.

Whenever these conditions are not met, the integral is said to be improper.

Integration Over an Infinite Interval

This type of improper integral arises when the integration interval extends to infinity:

$$ \int_a^{+\infty} f(x) \: dx $$

Example. In this case, the integrand is bounded, but the interval of integration is unbounded: [a, ∞).

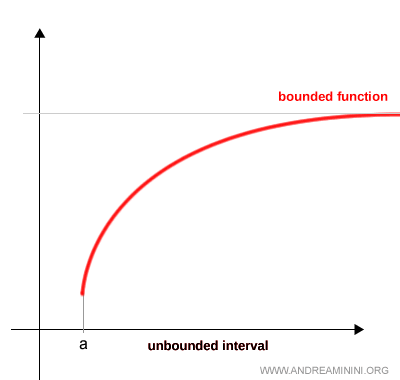
In such cases, the improper integral is defined as the limit of a definite integral as the upper bound approaches infinity:

$$ \int_a^{+\infty} f(x) \: dx = \lim_{b \to +\infty} \int_a^b f(x) \: dx $$

Equivalently, applying the Fundamental Theorem of Calculus:

$$ \int_a^{+\infty} f(x) \: dx = \lim_{b \to +\infty} [F(x)]_a^b $$

The convergence of the integral depends on the behavior of this limit:

• If the limit exists and is finite, the integral is convergent.
• If the limit exists but diverges to infinity, the integral is divergent.
• If the limit does not exist, the integral is oscillatory.

Justification: Limit Interpretation

Assume \( f(x) \) is continuous and non-negative on [a, ∞):

$$ \int_a^{+\infty} f(x) \: dx = \lim_{b \to +\infty} \int_a^b f(x) \: dx = \lim_{b \to +\infty} \left( F(b) - F(a) \right) $$

Since \( F(a) \) is constant, the behavior of the integral depends entirely on:

$$ \lim_{b \to +\infty} F(b) $$

Note. Here, \( F(b) \) is the antiderivative of \( f(x) \) evaluated at the upper limit: $$ F'(b) = f(b) $$

Because \( f(b) \ge 0 \), we have \( F'(b) \ge 0 \), so \( F(b) \) is non-decreasing over [a, ∞).

Therefore, the limit \( \lim_{b \to +\infty} F(b) \) exists (though it may be infinite), and so:

$$ \int_a^{+\infty} f(x) \: dx = \lim_{b \to +\infty} \int_a^b f(x) \: dx $$

Example 1

This is an improper integral because the upper limit is infinite:

$$ \int_1^{+\infty} \frac{1}{x^2} \: dx $$

We evaluate the limit:

$$ \lim_{b \to +\infty} \int_1^b \frac{1}{x^2} \: dx $$

The antiderivative of \( \frac{1}{x^2} \) is \( -\frac{1}{x} \), so:

$$ \lim_{b \to +\infty} \left[ -\frac{1}{x} \right]_1^b = \lim_{b \to +\infty} \left( -\frac{1}{b} + 1 \right) = 1 $$

Therefore, the integral converges and its value is 1.

Note. In general, for $$ \int_1^{+\infty} \frac{1}{x^k} \: dx $$ the integral converges if \( k > 1 \), and $$ \lim_{b \to +\infty} \left( \frac{b^{1-k}}{1-k} + \frac{1}{k-1} \right) = \frac{1}{k-1} $$ It diverges if \( k \le 1 \).

Example 2

$$ \int_1^{+\infty} \cos x \: dx $$

$$ = \lim_{b \to +\infty} \int_1^b \cos x \: dx = \lim_{b \to +\infty} [\sin x]_1^b $$

This limit does not exist because \( \sin b \) oscillates as \( b \to \infty \).

Therefore, the integral is oscillatory.

Unbounded Integrands on a Finite Interval

This second category of improper integrals involves functions that become unbounded at one endpoint of a finite interval:

$$ \int_a^b f(x) \: dx $$

Note. For example, the function may be defined over a finite interval but not continuous at one of its endpoints - say, it diverges as \( x \to b^- \). In this case, the function is defined on [a, b), not [a, b].

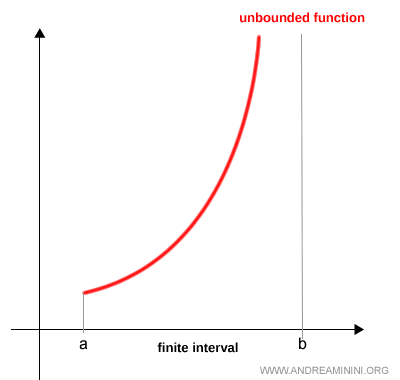
To handle this, we define the improper integral as a limit, introducing a small parameter \( h \to 0^+ \) to avoid the singularity:

$$ \int_a^b f(x) \: dx = \lim_{h \to 0^+} \int_{a+h}^b f(x) \: dx $$

Now the function is well-defined over [a + h, b].

Note. If the singularity were at the upper limit instead, we would write: $$ \int_a^b f(x) \: dx = \lim_{h \to 0^+} \int_a^{b - h} f(x) \: dx $$ The idea is the same: we approach the problematic endpoint from within the domain.

The convergence of the integral is again determined by the limit:

• If the limit exists and is finite, the integral is convergent.
• If the limit exists and diverges, the integral is divergent.
• If the limit does not exist, the integral is oscillatory.

Example

This integrand is bounded over the interval (0, 1], but is not defined at the lower endpoint:

$$ \int_0^1 \frac{1}{\sqrt{x}} \: dx $$

Note. Since the function is undefined at \( x = 0 \), we cannot compute the integral directly. Instead, we evaluate: $$ \int_0^1 \frac{1}{\sqrt{x}} \: dx = \lim_{h \to 0^+} \int_h^1 \frac{1}{\sqrt{x}} \: dx $$

The antiderivative of \( \frac{1}{\sqrt{x}} \) is \( 2\sqrt{x} \), so:

$$ = \lim_{h \to 0^+} [2\sqrt{x}]_h^1 = 2\sqrt{1} - 2\sqrt{0} = 2 - 0 = 2 $$

The limit exists and equals 2, so the improper integral converges:

$$ \int_0^1 \frac{1}{\sqrt{x}} \: dx = 2 $$

And that completes the evaluation.