Integral of a Composite Function Times the Derivative of Its Inner Function

The indefinite integral of a composite function f(g(x)) multiplied by the derivative of its inner function g(x) equals the antiderivative of f(g(x)). $$ \int f(g(x)) \cdot g'(x) \: dx = F(g(x)) + k $$

This is essentially the reverse process of the chain rule in differentiation.

This rule provides a powerful tool for evaluating a broad class of integrals involving composite functions.

A Practical Example

Consider the following indefinite integral:

$$ \int 2x \cdot \sin x^2 \: dx $$

We can recognize sin x² as a composite function f(g(x)), where:

$$ f(g(x)) = \sin x^2 $$

$$ g(x) = x^2 $$

Clearly, 2x is the derivative of the inner function g(x), which confirms the structure matches our integration rule.

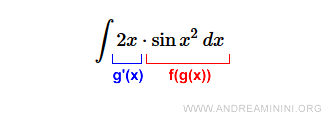
Now we apply the rule for integrating a composite function times the derivative of its inner argument:

$$ \int f(g(x)) \cdot g'(x) \: dx = F(g(x)) + k $$

$$ \int \sin x^2 \cdot 2x \: dx = F(g(x)) + k $$

Note. The antiderivative of the composite function f(g(x)) = sin x² is \( F(g(x)) = -\cos x^2 \). To verify this result, we differentiate F(g(x)) using the chain rule: $$ D[F(g(x))] = F'(g(x)) \cdot g'(x) $$ $$ D[F(g(x))] = D[- \cos x^2] \cdot D[x^2] $$ $$ D[F(g(x))] = \sin x^2 \cdot 2x $$ which matches the original integrand.

Therefore, we conclude:

$$ \int \sin x^2 \cdot 2x \: dx = - \cos x^2 + k $$

And the integral is fully evaluated.

Explanation and Justification

According to the chain rule for derivatives:

$$ D[f(g(x))] = f'(g(x)) \cdot g'(x) $$

In integration, we know that:

$$ \int h'(x) \: dx = h(x) + k $$

If we treat \( h'(x) \) as \( f'(g(x)) \cdot g'(x) \), then we can integrate directly:

$$ \int f'(g(x)) \cdot g'(x) \: dx = f(g(x)) + k $$

And that completes the reasoning.