Additive Property of Definite Integrals

If a function $ f(x) $ is Riemann integrable over the interval [a, c], and this interval is divided into two adjacent subintervals [a, b] and [b, c], then the definite integral of $ f(x) $ over [a, c] is equal to the sum of the integrals over the two parts: $$ \int_a^c f(x) \:dx = \int_a^b f(x) \:dx + \int_b^c f(x) \:dx $$

Geometrically, this means that the areas $ A_1 $ and $ A_2 $ under the curve $ f(x) $ are additive.

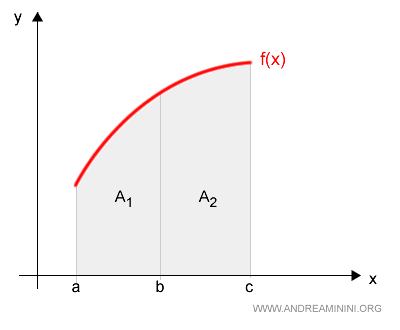
sum of the areas under the curve of the function

Proof

If the point $ b $ lies strictly between $ a $ and $ c $, we can define two partitions:

$$ P_1 = [a, b] \qquad P_2 = [b, c] $$

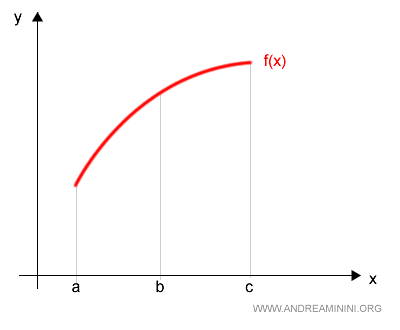
two separate partitions of the interval

The union of these partitions yields the full partition $ P $:

$$ P = P_1 \cup P_2 = [a, b] \cup [b, c] $$

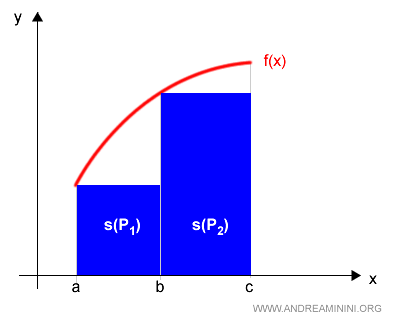
Accordingly, the lower Darboux sum over the entire interval satisfies:

$$ s(P) = s(P_1) + s(P_2) $$

lower Darboux sums for the two partitions

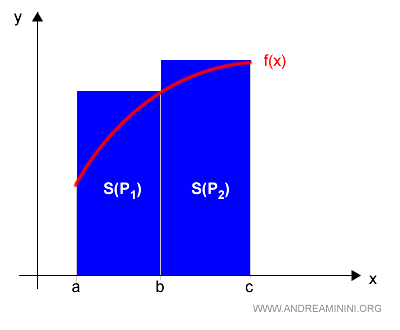
And similarly, the upper Darboux sum is:

$$ S(P) = S(P_1) + S(P_2) $$

upper Darboux sums for the two partitions

Therefore, by the definition of the Riemann integral, we conclude:

$$ \int_a^c f(x) \:dx = \int_a^b f(x) \:dx + \int_b^c f(x) \:dx $$

Note: When $ a = b $, the integral over [a, b] vanishes, so the formula simplifies to $$ \int_a^c f(x) \:dx = \int_a^b f(x) \:dx + \int_b^c f(x) \:dx = 0 + \int_b^c f(x) \:dx $$ Likewise, when $ a = c $, the integral over [a, c] evaluates to zero: $$ \int_a^c f(x) \:dx = \int_a^b f(x) \:dx - \int_b^a f(x) \:dx = 0 $$

And so on.