Integral Calculation Exercise 41

We are tasked with evaluating the following integral:

$$ \int \frac{2x+5}{(x+1) \cdot (x+3)^2 } \ dx $$

This is a rational function where the degree of the numerator is lower than that of the denominator, so there’s no need to perform polynomial division.

To solve it, we'll apply the method of partial fraction decomposition.

The denominator has two roots: $ x = -1 $, which is simple, and $ x = -3 $, which is a repeated root of multiplicity two.

Accordingly, we decompose the integrand as follows:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \ dx $$

We now write the right-hand side with a common denominator:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \frac{A(x+3)^2 + B(x+1)(x+3) + C(x+1)}{(x+1)(x+3)^2} \ dx $$

Expanding the numerator:

$$ A(x^2 + 6x + 9) + B(x^2 + 4x + 3) + Cx + C $$

Combining like terms:

$$ (A + B)x^2 + (6A + 4B + C)x + (9A + 3B + C) $$

Since the denominators match, we equate the numerators:

$ 2x + 5 = (A + B)x^2 + (6A + 4B + C)x + (9A + 3B + C) $

Comparing coefficients term by term:

From $ x^2 $: $ A + B = 0 $
From $ x $: $ 6A + 4B + C = 2 $
Constant term: $ 9A + 3B + C = 5 $

Explanation. Matching the coefficients of powers of $ x $, we get a system of three linear equations. The coefficient of $ x^2 $ on the left-hand side is 0, so $ A + B = 0 $, and so on.
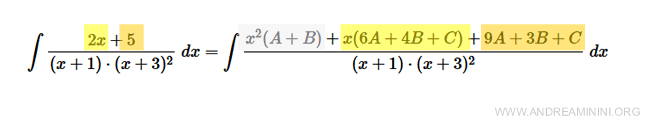
$explanation of partial fraction decomposition$

We now solve the system:

Substituting $ A = -B $ into the other two equations:

$$ \begin{cases} -2B + C = 2 \\ -6B + C = 5 \end{cases} $$

Subtracting the first from the second: $ (-6B + C) - (-2B + C) = 5 - 2 \Rightarrow -4B = 3 \Rightarrow B = -\frac{3}{4} $

Then: $ A = \frac{3}{4} $, $ C = 2 + 2B = 2 - \frac{3}{2} = \frac{1}{2} $

Thus, the constants are: A = 3/4, B = -3/4, C = 1/2.

We substitute these back into the integral:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \left( \frac{3}{4(x+1)} - \frac{3}{4(x+3)} + \frac{1}{2(x+3)^2} \right) dx $$

By the linearity of integration, we can integrate each term separately:

$$ = \frac{3}{4} \int \frac{1}{x+1} \ dx - \frac{3}{4} \int \frac{1}{x+3} \ dx + \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$

Each of these is a standard integral:

$ \int \frac{1}{x+1} \ dx = \log|x+1| + C $
$ \int \frac{1}{x+3} \ dx = \log|x+3| + C $
$ \int \frac{1}{(x+3)^2} \ dx = -\frac{1}{x+3} + C $

Putting it all together:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \frac{3}{4} \log|x+1| - \frac{3}{4} \log|x+3| - \frac{1}{2(x+3)} + C $$

Note. The last term comes from the power rule: $$ \frac{d}{dx}[-(x+3)^{-1}] = \frac{1}{(x+3)^2} $$

Therefore, the final result is:

$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \frac{3}{4} \log|x+1| - \frac{3}{4} \log|x+3| - \frac{1}{2(x+3)} + C $$

And that concludes the solution.