Integral Calculation Exercise 28

We are asked to evaluate the following integral:

$$ \int \frac{x^3+2x-3}{x^2+2x+1} \ dx $$

The integrand is a rational function - the quotient of two polynomials.

Since the degree of the numerator exceeds that of the denominator, we begin by performing polynomial division to simplify the expression.

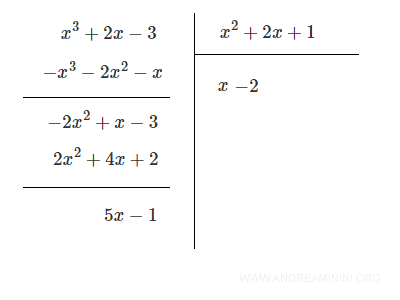
polynomial division example

The result of the division is:

$$ \frac{x^3+2x-3}{x^2+2x+1} = x - 2 \quad \text{with remainder } 5x - 1 $$

So we can rewrite the numerator as:

$$ x^3 + 2x - 3 = (x^2 + 2x + 1)(x - 2) + (5x - 1) $$

Substituting this into the original integral gives:

$$ \int \frac{(x^2+2x+1)(x - 2) + (5x - 1)}{x^2+2x+1} \ dx $$

We can now separate the expression into two simpler integrals using the linearity property:

$$ \int (x - 2) \ dx + \int \frac{5x - 1}{x^2 + 2x + 1} \ dx $$

The first integral is elementary:

$$ \frac{(x - 2)^2}{2} + c + \int \frac{5x - 1}{x^2 + 2x + 1} \ dx $$

Expanding and simplifying:

$$ \frac{x^2 - 4x + 4}{2} + c + \int \frac{5x - 1}{x^2 + 2x + 1} \ dx $$

$$ \frac{x^2}{2} - 2x + 2 + c + \int \frac{5x - 1}{x^2 + 2x + 1} \ dx $$

Since both $+2$ and $+c$ are constants, we can combine them into a single constant:

$$ \frac{x^2}{2} - 2x + c + \int \frac{5x - 1}{x^2 + 2x + 1} \ dx $$

We now focus on the remaining integral.

The integrand is a rational function that cannot be simplified further, as the denominator has higher degree than the numerator.

Note that the denominator is a perfect square:

$$ x^2 + 2x + 1 = (x + 1)^2 $$

This allows us to rewrite the integral as:

$$ \frac{x^2}{2} - 2x + c + \int \frac{5x - 1}{(x + 1)^2} \ dx $$

$$ \int \frac{5x - 1}{(x + 1)^2} \ dx = \int \frac{A}{(x + 1)^2} + \frac{B}{x + 1} \ dx $$

Combining the terms on the right-hand side gives:

$$ \int \frac{A + B(x + 1)}{(x + 1)^2} \ dx = \int \frac{A + Bx + B}{(x + 1)^2} \ dx $$

Since the denominators are the same, we match the numerators:

Comparing coefficients, we get:

$$ \begin{cases} B = 5 \\ A + B = -1 \end{cases} $$

Substituting $ B = 5 $ into the second equation gives $ A = -6 $.

Thus, the decomposition is:

$$ \int \frac{5x - 1}{(x + 1)^2} \ dx = \int \frac{-6}{(x + 1)^2} \ dx + \int \frac{5}{x + 1} \ dx $$

Factoring out the constants:

$$ = -6 \int \frac{1}{(x + 1)^2} \ dx + 5 \int \frac{1}{x + 1} \ dx $$

Both integrals are elementary:

So we have:

$$ \int \frac{5x - 1}{(x + 1)^2} \ dx = \frac{6}{x + 1} + 5 \log|x + 1| + c $$

Note. We verify this since $ \frac{d}{dx} \left( -\frac{1}{x + 1} \right) = \frac{1}{(x + 1)^2} $, confirming the antiderivative.

Substituting this result into the original expression, we obtain:

$$ \frac{x^2}{2} - 2x + \frac{6}{x + 1} + 5 \log|x + 1| + c $$

Therefore, the final solution is:

$$ \int \frac{x^3+2x-3}{x^2+2x+1} \ dx = \frac{x^2}{2} - 2x + \frac{6}{x + 1} + 5 \log|x + 1| + c $$

And that concludes the solution.