Integrating Rational Functions via Partial Fractions
Partial fraction decomposition is a powerful technique for integrating rational functions of the form $$ \int \frac{P(x)}{Q(x)} $$ where \( P(x) \) and \( Q(x) \) are polynomials, and the degree of \( P(x) \) is less than or equal to that of \( Q(x) \).
If the numerator \( P_n(x) \) has degree \( n \leq m \), where \( m \) is the degree of the denominator \( Q(x) \), we can write: $$ \int \frac{P(x)_n}{Q(x)_m} \ dx $$
Note. Any rational expression can be reduced, if necessary, through polynomial division to a form in which the numerator has lower or equal degree compared to the denominator. At that point, the method of partial fractions becomes applicable.
The decomposition depends on the nature of the roots of the denominator \( Q(x) \): whether they are real and distinct, repeated, or complex.
- Case 1: The denominator can be factored over the reals, i.e., into linear factors like \( (x - a) \), \( (x - a)^n \), or the general form \( ax + b \). For example, \( 3(x - 2) = 3x - 6 \).
- Each linear factor \( x - a \) corresponds to a partial fraction of the form $$ \frac{A}{x - a} $$
- Repeated linear factors \( (x - a)^n \) require a sum of terms with increasing powers in the denominator: $$ \frac{A}{x - a} + \frac{B}{(x - a)^2} + \dots + \frac{C}{(x - a)^n} $$
Note. Any quadratic polynomial of the form \( ax^2 + bx + c \) with real roots \( x_1 \) and \( x_2 \) (i.e., \( \Delta \geq 0 \)) can be factored as \( a(x - x_1)(x - x_2) \). For more on this, see factoring quadratic trinomials.
- Case 2: The denominator contains irreducible quadratic factors, i.e., polynomials with complex roots (when \( \Delta < 0 \)). Examples include \( x^2 + 1 \) or \( (x^2 + 1)^n \).
- Each irreducible quadratic factor gives rise to a partial fraction of the form $$ \frac{Ax + B}{ax^2 + bx + c} $$
- If the factor is repeated, the decomposition takes the form: $$ \frac{Ax + B}{ax^2 + bx + c} + \frac{Cx + D}{(ax^2 + bx + c)^2} + \dots + \frac{Ex + F}{(ax^2 + bx + c)^n} $$
To better illustrate how this works, let’s walk through a concrete example.
A] Denominator with Simple Real Roots
Consider the integral: $$ \int \frac{x - 1}{x^2 + 3x} \ dx $$
The integrand is a rational function where the degree of the numerator is less than that of the denominator, so polynomial division is not necessary.
We begin by factoring the denominator:
$$ \int \frac{x - 1}{x(x + 3)} \ dx $$
Both roots - \( x = 0 \) and \( x = -3 \) - have multiplicity one. This allows us to decompose the expression into a sum of simple fractions with undetermined coefficients:
$$ \int \frac{x - 1}{x(x + 3)} \ dx = \int \left( \frac{A}{x} + \frac{B}{x + 3} \right) dx $$
We now rewrite the right-hand side using a common denominator:
$$ \int \frac{x - 1}{x(x + 3)} \ dx = \int \frac{A(x + 3) + Bx}{x(x + 3)} \ dx $$
Simplifying the numerator:
$$ = \int \frac{(A + B)x + 3A}{x(x + 3)} \ dx $$
To identify the constants \( A \) and \( B \), we equate the numerators:
Left-hand side: \( x - 1 \) Right-hand side: \( (A + B)x + 3A \)
Matching coefficients yields the system: $$ \begin{cases} A + B = 1 \\ 3A = -1 \end{cases} $$
Solving:
From the second equation, \( A = -\frac{1}{3} \). Substituting into the first: \( -\frac{1}{3} + B = 1 \Rightarrow B = \frac{4}{3} \)
Thus: \( A = -\frac{1}{3} \), \( B = \frac{4}{3} \)
Substituting back into the integral:
$$ \int \frac{x - 1}{x(x + 3)} \ dx = \int \left( -\frac{1}{3x} + \frac{4}{3(x + 3)} \right) dx $$
By the linearity of integration:
$$ = -\frac{1}{3} \int \frac{1}{x} \ dx + \frac{4}{3} \int \frac{1}{x + 3} \ dx $$
Each term is a standard logarithmic integral:
$$ \int \frac{1}{x} \ dx = \log|x| + c \quad , \quad \int \frac{1}{x + 3} \ dx = \log|x + 3| + c $$
Therefore, the final result is:
$$ \int \frac{x - 1}{x(x + 3)} \ dx = -\frac{1}{3} \log|x| + \frac{4}{3} \log|x + 3| + c $$
This completes the integration using the method of partial fractions.
B] Denominator with a Root of Multiplicity 2
Let’s evaluate the integral:
$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx $$
The denominator has two distinct real roots: \( x = -1 \), which has multiplicity 1, and \( x = -3 \), which has multiplicity 2.
Accordingly, the decomposition must include terms for each power of the repeated factor:
$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \left( \frac{A}{x+1} + \frac{B}{x+3} + \frac{C}{(x+3)^2} \right) dx $$
Bringing everything to a common denominator:
$$ = \int \frac{A(x+3)^2 + B(x+1)(x+3) + C(x+1)}{(x+1)(x+3)^2} \ dx $$
Expanding the numerator:
$$ = \int \frac{A(x^2 + 6x + 9) + B(x^2 + 4x + 3) + Cx + C}{(x+1)(x+3)^2} \ dx $$
Combining like terms:
$$ = \int \frac{(A + B)x^2 + (6A + 4B + C)x + (9A + 3B + C)}{(x+1)(x+3)^2} \ dx $$
Equating numerators with the original expression \( 2x + 5 \), we obtain:
Explanation. Comparing coefficients: • \( x^2 \) term: \( A + B = 0 \) • \( x \) term: \( 6A + 4B + C = 2 \) • Constant term: \( 9A + 3B + C = 5 \)
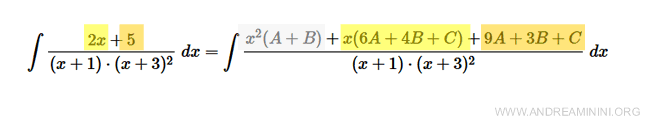
Solving the system:
From \( A + B = 0 \), we get \( A = -B \). Substituting:
$$ \begin{cases} -2B + C = 2 \\ -6B + C = 5 \end{cases} $$
Subtracting the equations gives:
$$ -4B = 3 \Rightarrow B = -\frac{3}{4}, \quad A = \frac{3}{4}, \quad C = \frac{1}{2} $$
Substituting these values into the decomposition:
$$ \int \frac{2x+5}{(x+1)(x+3)^2} \ dx = \int \left( \frac{3}{4(x+1)} - \frac{3}{4(x+3)} + \frac{1}{2(x+3)^2} \right) dx $$
By the linearity of integration:
$$ = \frac{3}{4} \int \frac{1}{x+1} \ dx - \frac{3}{4} \int \frac{1}{x+3} \ dx + \frac{1}{2} \int \frac{1}{(x+3)^2} \ dx $$
The first two integrals yield logarithms, while the third is a power function:
$$ = \frac{3}{4} \log|x+1| - \frac{3}{4} \log|x+3| - \frac{1}{2(x+3)} + C $$
Note. Since $$ \frac{d}{dx}[-(x+3)^{-1}] = \frac{1}{(x+3)^2}, $$ it follows that $$ \int \frac{1}{(x+3)^2} \ dx = -\frac{1}{x+3} $$
This completes the integration.
C] Denominator with Complex Roots
Now evaluate:
$$ \int \frac{x-1}{x(x^2+1)} \ dx $$
The denominator consists of one real root, \( x = 0 \), and a pair of complex conjugate roots from \( x^2 + 1 \).
We use the following decomposition:
$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \left( \frac{A}{x} + \frac{Bx+C}{x^2+1} \right) dx $$
Writing the right-hand side with a common denominator:
$$ = \int \frac{A(x^2+1) + x(Bx + C)}{x(x^2+1)} \ dx $$
Expanding the numerator:
$$ = \int \frac{(A + B)x^2 + Cx + A}{x(x^2+1)} \ dx $$
Equating numerators with the original expression \( x - 1 \):
$$ A + B = 0,\quad C = 1,\quad A = -1 $$
Solving: \( A = -1, \quad B = 1, \quad C = 1 \)
Substituting back:
$$ \int \frac{x-1}{x(x^2+1)} \ dx = \int \left( -\frac{1}{x} + \frac{x+1}{x^2+1} \right) dx $$
Splitting the integrand:
$$ = - \int \frac{1}{x} \ dx + \int \frac{x}{x^2+1} \ dx + \int \frac{1}{x^2+1} \ dx $$
Each term is now straightforward:
- $$ \int \frac{1}{x} \ dx = \log|x| + C $$
- $$ \int \frac{x}{x^2+1} \ dx = \frac{1}{2} \log(x^2+1) $$
- $$ \int \frac{1}{x^2+1} \ dx = \arctan(x) $$
Note. To compute $$ \int \frac{x}{x^2+1} \ dx, $$ observe that $$ \frac{d}{dx} \log(x^2+1) = \frac{2x}{x^2+1} \Rightarrow \frac{1}{2} \log(x^2+1) $$ is the antiderivative.
The final result is:
$$ \int \frac{x-1}{x(x^2+1)} \ dx = -\log|x| + \frac{1}{2} \log(x^2+1) + \arctan(x) + C $$
And the integral is complete.
And so on.
