Involutory Transformations in Geometry
An involutory transformation in geometry (or involution) is a transformation that, when applied twice, returns the object to its original state, essentially acting as an identity transformation.
In simpler terms, it's a transformation \( T \) that, when applied consecutively to a geometric object (e.g., a plane figure, solid, etc.), brings the object back to its starting position.
Mathematically, an involutory transformation can be described as a function that, when applied to any point \( x \), returns the point itself.
$$ T(T(x)) = x $$
Involutory transformations are found in various branches of geometry, such as Euclidean geometry, projective geometry, and algebraic geometry, and they possess several intriguing properties.
Here are some common examples of involutory geometric transformations:
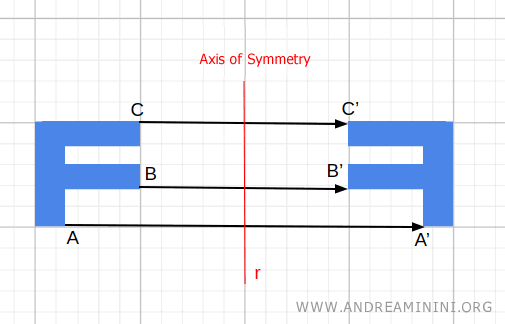
- Reflection (Axial Symmetry)
Reflecting an object across a line (in the plane) or a plane (in space) is a classic example of an involutory transformation. If you reflect the object twice across the same line or plane, every point returns to its original position.
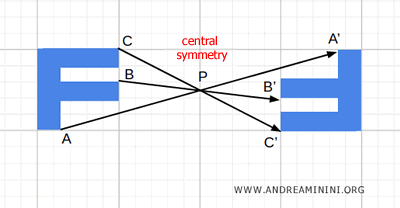
- Central Symmetry
Central symmetry around a point is another example of an involutory transformation. When you apply the same central symmetry to a point twice, it returns to its original position.
Involutory Transformations in Analytic Geometry
A transformation \( t \) is said to be involutory if it is equal to its own inverse: \( t = t^{-1} \).
In other words, applying the transformation twice in succession results in the identity transformation, which leaves every point unchanged.
$$t \circ t = i $$
Here, \( i \) denotes the identity transformation.
This property means that the transformation effectively undoes itself: \( t \circ t = i \Leftrightarrow t = t^{-1} \).
Example
Consider the transformation \( t \) defined by the following system of equations:
$$ t: \begin{cases} x' = -x \\ \\ y' = -y \end{cases} $$
This transformation maps any point \( P(x, y) \) to its reflection through the origin, \( P'(-x, -y) \).
If we apply the transformation a second time, we get:
- \( P(x, y) \mapsto P'(-x, -y) \)
- \( P'(-x, -y) \mapsto P''(x, y) = P \)
Therefore, \( t \circ t = i \): the transformation \( t \) is involutory because it returns each point to its original position.
For example, applying \( t \) to the point \( P(1, 2) \) yields:
- \( P(1, 2) \mapsto P'(-1, -2) \)
- \( P'(-1, -2) \mapsto P''(1, 2) \)
The final point \( P'' \) coincides with the original point \( P(1, 2) \).

In essence, applying the transformation twice has no net effect.
And so on.
