Subtracting Complex Numbers

The difference between two complex numbers is another complex number, where the real part is the difference of the real parts, and the imaginary part is the difference of the imaginary coefficients. $$ (a - bi) - (c - di) = (a - c) + (b - d)i $$

An Example

Let’s consider two complex numbers, \( z_1 \) and \( z_2 \).

$$ z_1 = 5 + 6i $$

$$ z_2 = 2 + 4i $$

Now, we subtract \( z_2 \) from \( z_1 \).

$$ z_1 - z_2 = (5 + 6i) - (2 + 4i) $$

We subtract the real and imaginary parts separately:

$$ z_1 - z_2 = 5 + 6i - 2 - 4i $$

$$ z_1 - z_2 = (5 - 2) + (6i - 4i) $$

$$ z_1 - z_2 = 3 + 2i $$

So, the result of \( z_1 - z_2 \) is the complex number \( 3 + 2i \).

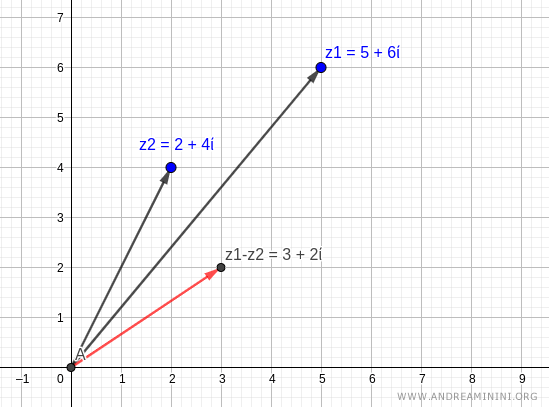
Note. Complex numbers can also be represented as coordinates in the Gaussian plane (x, y) or as two-dimensional vectors. For example, the numbers \( z_1 \) and \( z_2 \) correspond to the following coordinate pairs (or vectors): $$ z_1 = 5 + 6i = (5,6) $$ $$ z_2 = 2 + 4i = (2,4) $$ Now, we compute their difference as vectors: $$ z_1 - z_2 = (5,6) - (2,4) $$ $$ z_1 - z_2 = (5 - 2, 6 - 4) $$ $$ z_1 - z_2 = (3,2) $$ As expected, the result is the same.

Proof

Let’s define two complex numbers, \( z_1 \) and \( z_2 \):

$$ z_1 = a + bi $$

$$ z_2 = c + di $$

Now, we calculate their difference:

$$ z_1 - z_2 = (a + bi) - (c + di) $$

$$ z_1 - z_2 = a + bi - c - di $$

Applying the associative and distributive properties:

$$ z_1 - z_2 = (a - c) + (bi - di) $$

$$ z_1 - z_2 = (a - c) + i(b - d) $$

Thus, the result is another complex number, where the real part is \( a - c \) and the imaginary part is \( (b - d)i \).

Additional Notes

Here are some additional observations about subtracting complex numbers:

• Subtracting Conjugate Complex Numbers
  The difference between two conjugate complex numbers, \( z_1 = a + bi \) and \( z_2 = a - bi \), is a purely imaginary number: $$ z_1 - z_2 = (a + bi) - (a - bi) = a + bi - a + bi = 2bi $$ The result consists solely of the imaginary part, doubled, with a coefficient of \( 2b \). This happens because the real parts cancel out, leaving only the imaginary component.

  Example. Let’s take the complex numbers \( z_1 = 3 + 4i \) and \( z_2 = 3 - 4i \) and compute their difference: $$ z_1 - z_2 = (3 + 4i) - (3 - 4i) = 3 + 4i - 3 + 4i = 8i $$ As expected, the result is the purely imaginary number \( 8i \), which is exactly twice the imaginary coefficient of \( z_1 \), which is \( 4 \).

And so on.