Cosine subtraction formula

The cosine subtraction formula is $$ \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $$

Therefore, it’s never correct to write:

$$ \cos (\alpha - \beta) = \cos \alpha - \cos \beta $$

A practical example

The cosine of 90° (π/2) is 1, while the cosine of 60° (π/3) is 1/2:

$$ \cos \frac{\pi}{2} = 1 $$

$$ \cos \frac{\pi}{3} = \frac{1}{2} $$

Now, I need to calculate the cosine of the difference between 90° and 60°:

$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) $$

Using the cosine subtraction formula with α = π/2 and β = π/3, we get:

$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = \cos \frac{\pi}{2} \cos \frac{\pi}{3} + \sin \frac{\pi}{2} \sin \frac{\pi}{3} $$

$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = 0 \cdot \frac{1}{2} + 1 \cdot \frac{\sqrt{3}}{2} $$

$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = \frac{\sqrt{3}}{2} $$

Note: Notice that $$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) \ne \cos ( \frac{\pi}{2} ) - \cos ( \frac{\pi}{3} ) = 1 - \frac{1}{2} $$

Verification

$$ \cos ( \frac{\pi}{2} - \frac{\pi}{3} ) = \cos ( \frac{3\pi - 2 \pi}{6} ) = \cos ( \frac{\pi}{6} ) = \frac{ \sqrt{3} }{2} $$

The proof

Let’s draw two angles, α and β, on a unit circle, with α > β.

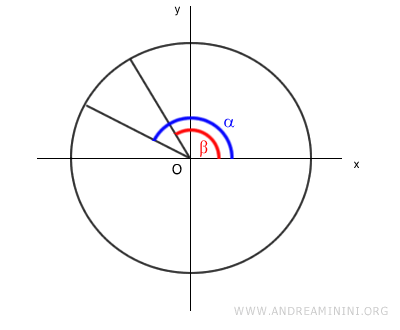
The difference between α and β is the angle α - β:

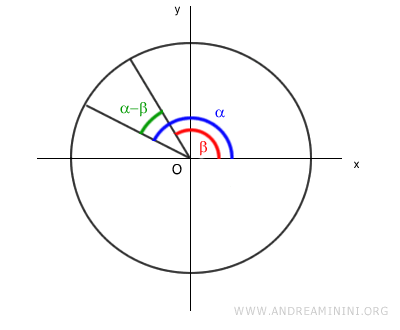
Now, let’s consider the same angle α - β, but starting from the origin side:

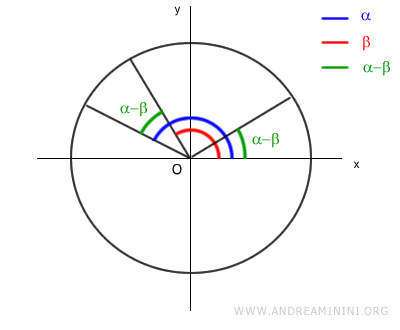
Triangles OAB and OCD are congruent (identical) because they share the same angles and side lengths:

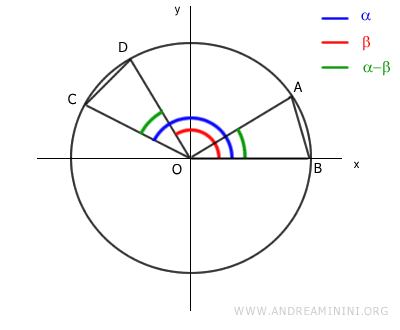
Thus, segments AB and CD are of equal length:

$$ \overline{AB} = \overline{CD} $$

This means the distance between points A and B is the same as the distance between points C and D:

$$ \overline{AB}^2 = (x_A - x_B)^2 + (y_A - y_B)^2 $$

$$ \overline{CD}^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$

Since the distances are the same, we can write:

$$ \overline{AB}^2 = \overline{CD}^2 $$

$$ (x_A - x_B)^2 + (y_A - y_B)^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$

Next, we substitute the x and y coordinates with their corresponding trigonometric functions:

We know that x_A = cos(α - β) and y_A = sin(α - β):

$$ (\cos(α-β) - x_B)^2 + (\sin(α-β) - y_B)^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$

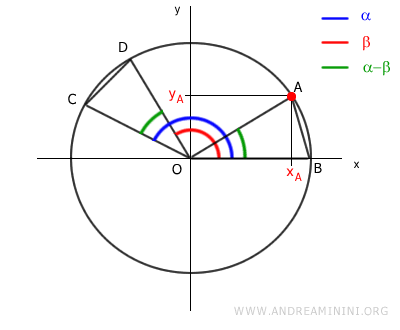
Since x_B = cos(0) = 1 and y_B = sin(0) = 0, we have:

$$ (\cos(α-β) - 1)^2 + (\sin(α-β) - 0)^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$

$$ (\cos(α-β) - 1)^2 + (\sin(α-β))^2 = (x_C - x_D)^2 + (y_C - y_D)^2 $$

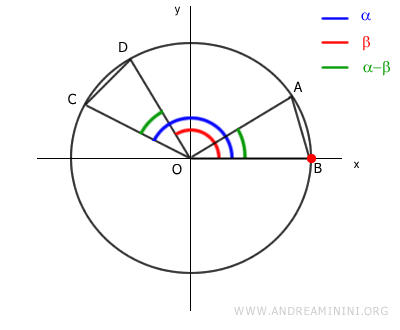
Now, knowing that x_C = cos(α) and y_C = sin(α),

$$ (\cos(α-β) - 1)^2 + (\sin(α-β))^2 = ( \cos(α) - x_D)^2 + ( \sin(α) - y_D)^2 $$

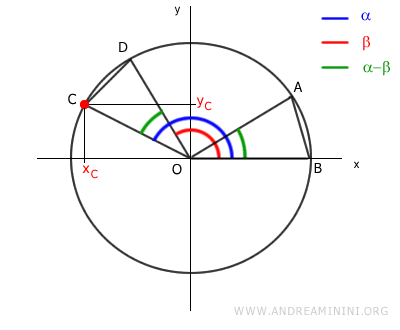
Since x_D = cos(β) and y_D = sin(β),

$$ (\cos(α-β) - 1)^2 + (\sin(α-β))^2 = (\cos(α) - \cos(β) )^2 + (\sin(α) - \sin(β))^2 $$

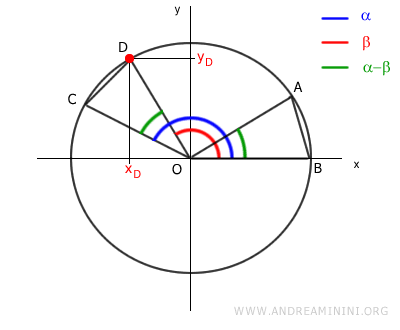
Now we simplify and expand the binomials:

$$ \cos^2(α-β) - 2 \cos(α-β) + 1^2 + \sin^2(α-β) = \cos^2(α) - 2 \cos(α) \cos(β) + \cos^2(β) + \\ + \sin^2(α) - 2 \sin(α) \sin(β) + \sin^2(β) $$

$$ \cos^2(α-β) - 2 \cos(α-β) + 1 + \sin^2(α-β) = \cos^2(α) - 2 \cos(α) \cos(β) + \cos^2(β) + \\ + \sin^2(α) - 2 \sin(α) \sin(β) + \sin^2(β) $$

According to the Pythagorean identity, the sum of the squares of sine and cosine for any angle is equal to 1:

$$ [ \cos^2(α-β) + \sin^2(α-β) ] - 2 \cos(α-β) + 1 = [ \cos^2(α) + \sin^2(α) ] - 2 \cos(α) \cos(β) + \\ - 2 \sin(α) \sin(β) + [ \cos^2(β) + \sin^2(β) ] $$

$$ 1 - 2 \cos(α-β) + 1 = 1 - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) + 1 $$

Thus, we get:

$$ 2 - 2 \cos(α-β) = 2 - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) $$

Subtract 2 from both sides:

$$ 2 - 2 \cos(α-β) \color{red}{- 2} = 2 - 2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) \color{red}{- 2} $$

$$ -2 \cos(α-β) = -2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) $$

Multiply both sides by -1 to get positive values:

$$ -1 \cdot [ -2 \cos(α-β) ] = -1 \cdot [ -2 \cos(α) \cos(β) - 2 \sin(α) \sin(β) ] $$

$$ 2 \cos(α-β) = 2 \cos(α) \cos(β) + 2 \sin(α) \sin(β) $$

Finally, divide by 2 to get the desired formula:

$$ \cos(α-β) = \cos(α) \cos(β) + \sin(α) \sin(β) $$

And there you have it!