How to Add Two Angles in Degrees, Minutes, and Seconds

When adding two angles in the sexagesimal system, you start by adding the seconds, followed by the minutes, and finally the degrees.

A Practical Example

Here’s a step-by-step explanation.

We have two angles expressed in degrees, minutes, and seconds:

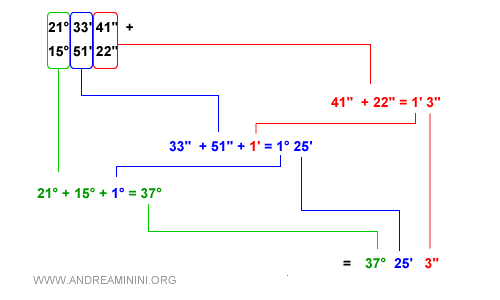
21° 33' 41"
15° 51' 22"

Now let's add them together:

21° 33' 41" + 15° 51' 22"

First, we add the seconds 41" + 22":

41" + 22" = 63"

Since the total seconds (63") are greater than 60, we convert the excess into minutes (1').

The remaining 3" are part of the final result.

41" + 22" = 1' 3"

Next, we add the minutes from both angles 33' + 51', including the 1' carried over from the seconds.

33' + 51' + 1' = 85'

Since the total minutes (85') are also greater than 60, we convert the excess into degrees (1°).

The remaining 25' are part of the final result.

33' + 51' + 1' = 1° 25'

Finally, we add the degrees from both angles 21° + 15°, plus the 1° carried over from the minutes.

21° + 15° + 1° = 37°

Now we combine the degrees, minutes, and seconds to get the final result:

37° 25' 3"

And that’s how you add two angles using the sexagesimal system!