How to calculate a triangle's angles and sides using trigonometry

To solve a triangle using trigonometry, you need to know at least:


• one side and two angles
• two sides and the angle between them (or opposite one of the sides)
• all three sides

Solving a triangle involves finding the lengths of its sides and the measures of its angles.

A practical example

Depending on the information available, you can follow different methods.

Example 1

In this example, we know the length of one side and the measures of two angles.

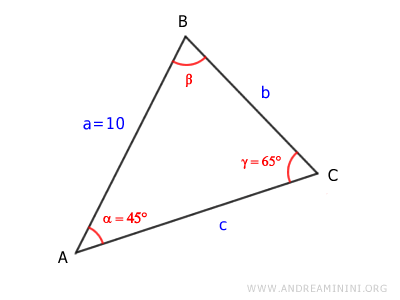
The given side length is:

$$ \overline{AB} = 10 $$

The known angles are:

$$ \alpha = 45° $$

$$ \gamma = 65° $$

Since the sum of a triangle's angles is always 180° (π radians):

$$ \alpha + \beta + \gamma = 180° $$

We find the missing angle by subtracting the two known angles:

$$ \beta = 180° - \alpha - \gamma $$

$$ \beta = 180° - 45° - 65° $$

$$ \beta = 70° $$

Thus, the missing angle is β = 70°.

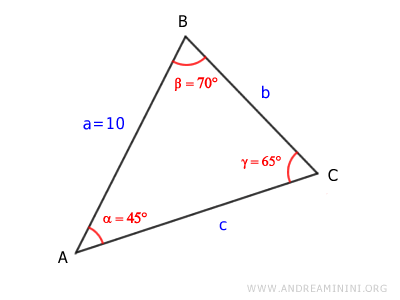
Now we can calculate the remaining sides using the Law of Sines, which states that each side of a triangle is proportional to the sine of its opposite angle:

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$

To find the length of side BC, we use AB = 10, γ = 65°, and α = 45°:

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} $$

$$ \frac{10}{\sin 65°} = \frac{\overline{BC}}{\sin 45°} $$

$$ \overline{BC} = \frac{10}{\sin 65°} \cdot \sin 45° $$

$$ \overline{BC} = 7.802 $$

Next, to find side AC, we use AB = 10, γ = 65°, and β = 70°:

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{AC}}{\sin \beta} $$

$$ \frac{10}{\sin 65°} = \frac{\overline{AC}}{\sin 70°} $$

$$ \overline{AC} = \frac{10}{\sin 65°} \cdot \sin 70° $$

$$ \overline{AC} = 10.368 $$

So, the lengths of the remaining sides are BC = 7.802 and AC = 10.368.

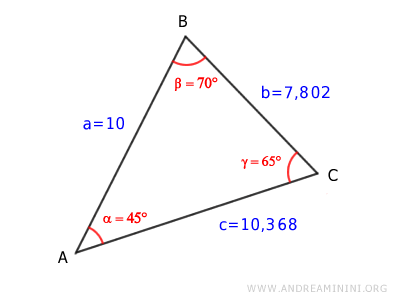
With all the angles and sides known, the triangle is fully solved.

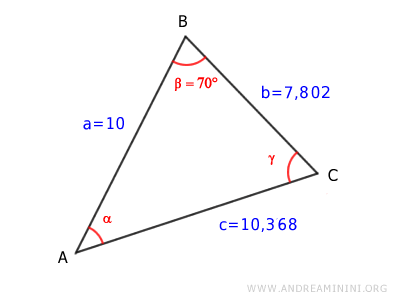
Example 2

In this example, we know the lengths of two sides and the angle between them.

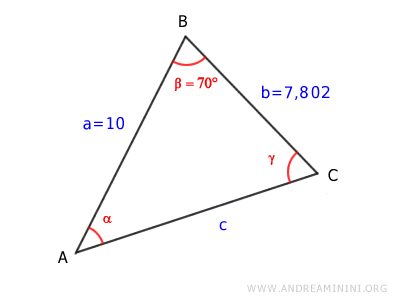
The side lengths are:

$$ \overline{AB} = 10 $$

$$ \overline{BC} = 7.802 $$

The included angle is:

$$ \beta = 70° $$

Here, we apply the Law of Cosines, which states that the square of one side (AC²) equals the sum of the squares of the other two sides (AB² + BC²) minus twice their product times the cosine of the included angle (β):

$$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 - 2 \cdot \overline{AB} \cdot \overline{BC} \cdot \cos \beta $$

Substituting AB = 10, BC = 7.802, and β = 70°:

$$ \overline{AC}^2 = 10^2 + 7.802^2 - 2 \cdot 10 \cdot 7.802 \cdot \cos 70° $$

$$ \overline{AC}^2 = 100 + 60.871 - 156.04 \cdot \cos 70° $$

$$ \overline{AC}^2 = 107.502 $$

Taking the square root:

$$ \overline{AC} = \sqrt{107.502} $$

$$ \overline{AC} = 10.368 $$

Thus, the missing side AC is 10.368.

To calculate the remaining angles α and γ, we again use the Law of Cosines. For γ, rearranging gives:

$$ \cos \gamma = \frac{\overline{BC}^2 + \overline{AC}^2 - \overline{AB}^2}{2 \cdot \overline{BC} \cdot \overline{AC}} $$

Substituting the known values:

$$ \cos \gamma = \frac{7.802^2 + 10.368^2 - 10^2}{2 \cdot 7.802 \cdot 10.368} $$

$$ \cos \gamma = 0.4226 $$

Using the inverse cosine function:

$$ \gamma = \arccos(0.4226) $$

$$ \gamma = 65° $$

Finally, since the angles of a triangle add up to 180°, we find α:

$$ \alpha = 180° - \beta - \gamma $$

$$ \alpha = 180° - 70° - 65° $$

$$ \alpha = 45° $$

With all the sides and angles determined, the triangle is now completely solved.

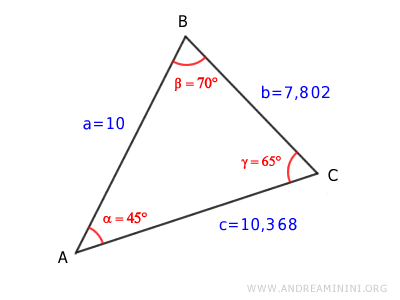
Note. Although the Law of Sines can also be used to calculate γ, the Law of Cosines is preferred here because it avoids ambiguity when dealing with sine values, which can correspond to two possible angles.

Example 3

In this example, we know the lengths of two sides and the angle opposite one of them.

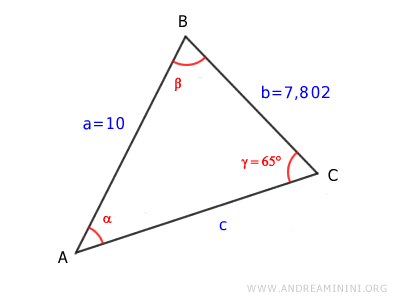
The given side lengths are:

$$ \overline{AB} = 10 $$

$$ \overline{BC} = 7.802 $$

The angle γ is opposite side AB:

$$ \gamma = 65° $$

To solve the triangle, we apply the Law of Sines:

$$ \frac{\overline{AB}}{\sin \gamma} = \frac{\overline{BC}}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$

$$ \frac{10}{\sin 65°} = \frac{7.802}{\sin \alpha} = \frac{\overline{AC}}{\sin \beta} $$

First, we calculate angle α:

$$ \frac{10}{\sin 65°} = \frac{7.802}{\sin \alpha} $$

$$ \sin \alpha = \frac{7.802}{10} \cdot \sin 65° $$

$$ \sin \alpha = 0.7071 $$

Using the arcsine function, we find:

$$ \alpha = \arcsin(0.7071) $$

$$ \alpha = 45° $$

Thus, angle α is 45°.

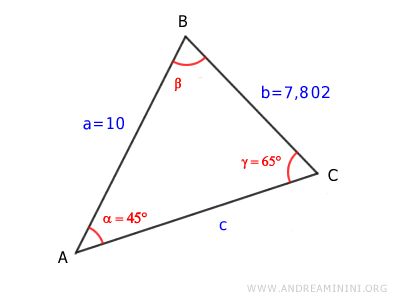
Note. The Law of Sines is reliable here because the sine value lies between 0 and 1, allowing us to determine an angle smaller than 90°. In some cases, this method may not be suitable.

Now that we know two angles, the third angle is easily calculated by subtracting their sum from 180°:

$$ \alpha + \beta + \gamma = 180° $$

$$ \beta = 180° - \alpha - \gamma $$

$$ \beta = 180° - 45° - 65° $$

$$ \beta = 70° $$

Thus, the remaining angle β is 70°.

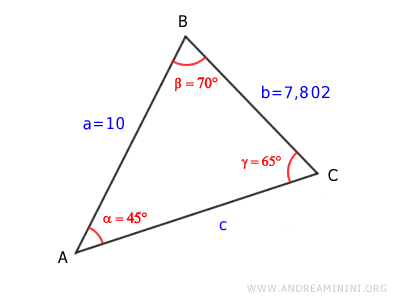
Finally, we calculate the length of side AC using the Law of Cosines:

$$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 - 2 \cdot \overline{AB} \cdot \overline{BC} \cdot \cos \beta $$

Substitute the known values:

$$ \overline{AC}^2 = 10^2 + 7.802^2 - 2 \cdot 10 \cdot 7.802 \cdot \cos 70° $$

$$ \overline{AC}^2 = 100 + 60.871 - 2 \cdot 78.02 \cdot \cos 70° $$

$$ \overline{AC}^2 = 160.84 - 156.04 \cdot \cos 70° $$

$$ \overline{AC}^2 = 107.502 $$

Taking the square root of both sides:

$$ \overline{AC} = \sqrt{107.502} $$

$$ \overline{AC} = 10.368 $$

The length of the missing side is AC = 10.368, completing the solution.

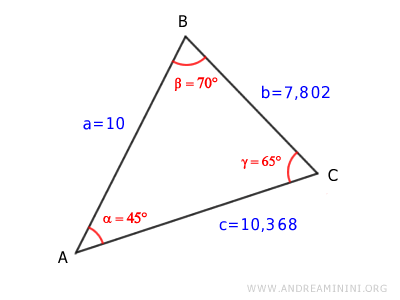
Example 4

In this example, we know the lengths of the triangle's three sides, but none of its angles.

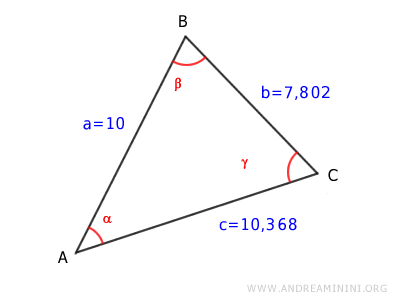
The side lengths are as follows:

$$ \overline{AB} = 10 $$

$$ \overline{BC} = 7.802 $$

$$ \overline{AC} = 10.368 $$

We begin by calculating angle β using the Law of Cosines:

$$ \overline{AC}^2 = \overline{AB}^2 + \overline{BC}^2 - 2 \cdot \overline{AB} \cdot \overline{BC} \cdot \cos \beta $$

Substitute the known values:

$$ 10.368^2 = 10^2 + 7.802^2 - 2 \cdot 10 \cdot 7.802 \cdot \cos \beta $$

$$ 107.495424 = 100 + 60.871204 - 156.04 \cdot \cos \beta $$

Reorganize to isolate the cosine term:

$$ 107.495424 - 100 - 60.871204 = -156.04 \cdot \cos \beta $$

$$ -53.37578 = -156.04 \cdot \cos \beta $$

Multiply both sides by -1:

$$ 53.37578 = 156.04 \cdot \cos \beta $$

Divide through by 156.04:

$$ \cos \beta = \frac{53.37578}{156.04} $$

$$ \cos \beta = 0.3421 $$

Now, use the arccosine function to find angle β:

$$ \beta = \arccos(0.3421) $$

$$ \beta = 70° $$

So, angle β measures 70°.

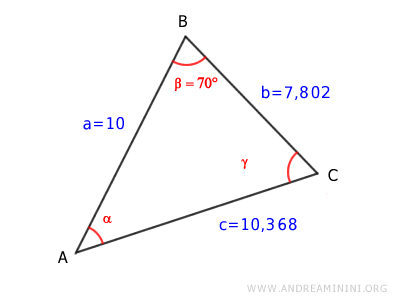
Next, we calculate angle α using the Law of Cosines again:

$$ \overline{BC}^2 = \overline{AB}^2 + \overline{AC}^2 - 2 \cdot \overline{AB} \cdot \overline{AC} \cdot \cos \alpha $$

Substitute the known values:

$$ 7.802^2 = 10^2 + 10.368^2 - 2 \cdot 10 \cdot 10.368 \cdot \cos \alpha $$

$$ 60.871204 = 100 + 107.495424 - 207.36 \cdot \cos \alpha $$

Isolate the cosine term:

$$ 60.871204 - 100 - 107.495424 = -207.36 \cdot \cos \alpha $$

$$ -146.62422 = -207.36 \cdot \cos \alpha $$

Multiply through by -1:

$$ 146.62422 = 207.36 \cdot \cos \alpha $$

Divide both sides by 207.36:

$$ \cos \alpha = \frac{146.62422}{207.36} $$

$$ \cos \alpha = 0.7071 $$

Using the arccosine function:

$$ \alpha = \arccos(0.7071) $$

$$ \alpha = 45° $$

Thus, angle α measures 45°.

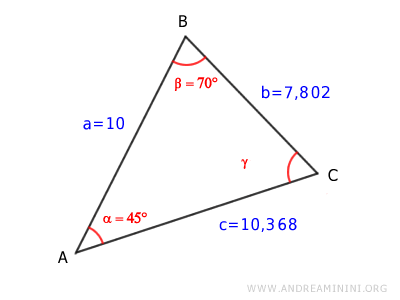
Finally, we calculate angle γ by subtracting the known angles from 180° (since the sum of a triangle's angles is always 180°):

$$ \alpha + \beta + \gamma = 180° $$

$$ \gamma = 180° - \alpha - \beta $$

$$ \gamma = 180° - 45° - 70° $$

$$ \gamma = 65° $$

So, angle γ measures 65°.

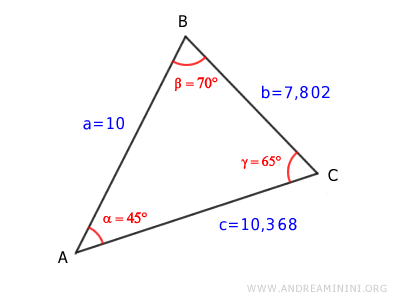
Now that we know all the sides and angles, the triangle is fully solved.

The solution is complete.