How to Calculate the Radius of a Triangle's Circumscribed Circle

The radius of a triangle's circumscribed circle can be calculated if you know one side of the triangle and the angle opposite that side. $$ r = \frac{ \overline{AB} }{2 \sin \alpha} $$ Here, AB is one side of the triangle, and alpha (α) is the angle opposite to it.

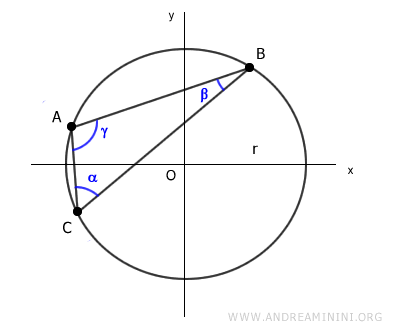
In the same way, you can find the radius using either of the other two sides, BC or AC, along with their respective opposite angles, gamma or beta.

$$ r = \frac{ \overline{BC} }{2 \sin \gamma} $$

$$ r = \frac{ \overline{AC} }{2 \sin \beta} $$

A Practical Example

Let’s take a triangle ABC with a circumscribed circle.

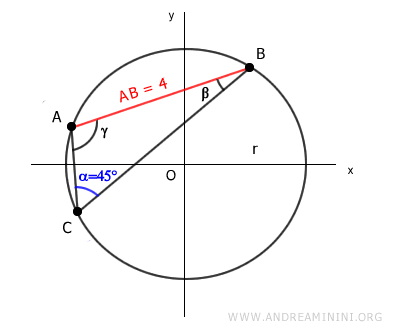
We don’t know the radius of the circle, but we do know the length of side AB and the measure of the opposite angle α:

$$ \overline{AB} = 4 $$

$$ \alpha = 45° $$

Using these two values, we can calculate the radius (r) of the circle:

$$ r = \frac{ \overline{AB} }{2 \sin \alpha} = \frac{ 4 }{2 \sin 45°} = \frac{ 4 }{2 \frac{\sqrt{2}}{2} } = \frac{ 4 }{\sqrt{2} } = 2.83 $$

Thus, the radius of the circle is 2.83.

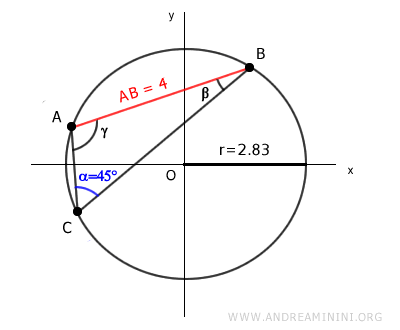
Note: The same result can be obtained by knowing the length of side AC and its opposite angle β, or the length of side BC and its opposite angle γ.

The Proof

Let’s analyze a circumscribed circle around triangle ABC.

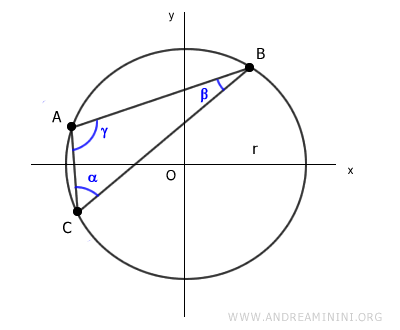
Each side of the triangle can be considered a chord of the circle.

For instance, side AB acts as a chord connecting two points on the circle.

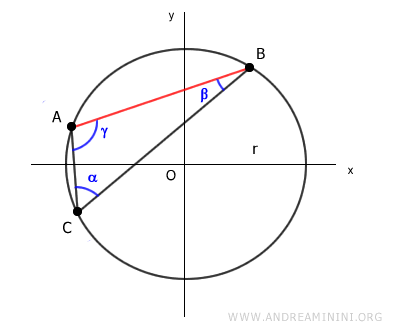
According to the chord theorem, the length of chord AB equals the circle's diameter (2r) multiplied by the sine of the angle (α) opposite to side AB.

$$ \overline{AB} = 2r \cdot \sin \alpha $$

By isolating the radius (r), we derive the formula:

$$ r = \frac{ \overline{AB} }{2 \sin \alpha} $$

We can prove the other formulas in the same manner.

Let’s now consider chord BC:

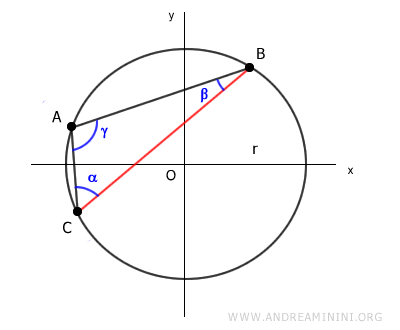
According to the chord theorem, the length of chord BC equals the circle's diameter (2r) multiplied by the sine of the angle (γ) opposite to side BC:

$$ \overline{BC} = 2r \cdot \sin \gamma $$

Isolating the radius (r), we get:

$$ r = \frac{ \overline{BC} }{2 \sin \gamma} $$

Finally, let’s analyze chord AC:

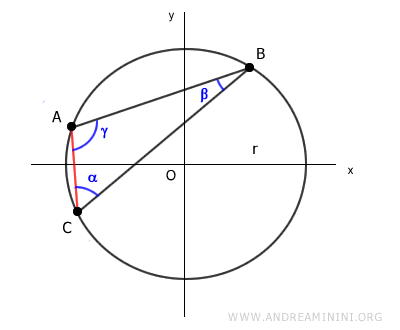
Again, using the chord theorem, the length of chord AC equals the circle's diameter (2r) multiplied by the sine of the angle (β) opposite to side AC:

$$ \overline{AC} = 2r \cdot \sin \beta $$

By isolating the radius (r), we obtain:

$$ r = \frac{ \overline{AC} }{2 \sin \beta} $$

And so on.