How to Simplify and Solve a Trigonometric Equation in Elementary Form

A trigonometric equation involving multiple trigonometric functions can often be rewritten as a simpler, elementary equation.

Convert all trigonometric functions in the equation to a single reference function (e.g., cosine).
Note: The choice of reference function depends on what simplifies the calculations. Sometimes cosine is the best option, but in other cases, sine or tangent may be more convenient.
Treat the reference trigonometric function as a variable.
Solve the equation, breaking it down into simpler trigonometric equations if needed.

A Practical Example

Consider the following equation:

$$ 3 \sin^2 x + 4 \cos x = 3 $$

This equation involves both sine and cosine functions.

In this case, it’s more convenient to use cosine as the reference function.

Using the first fundamental trigonometric identity:

$$ \sin^2 x + \cos^2 x = 1 $$

We can rewrite $ \sin^2 x $ in terms of cosine:

$$ \sin^2 x = 1 - \cos^2 x $$

Substituting $ \sin^2 x $ with $ 1 - \cos^2 x $ in the equation:

$$ 3 \sin^2 x + 4 \cos x = 3 $$

$$ 3 (1 - \cos^2 x) + 4 \cos x = 3 $$

$$ 3 - 3 \cos^2 x + 4 \cos x = 3 $$

This simplifies the equation to involve only the cosine function.

Subtract 3 from both sides to simplify further:

$$ 3 - 3 \cos^2 x + 4 \cos x - 3 = 3 - 3 $$

$$ - 3 \cos^2 x + 4 \cos x = 0 $$

To make the calculation easier, multiply both sides by (-1), reversing the signs:

$$ -1 \cdot ( -3 \cos^2 x + 4 \cos x ) = -1 \cdot 0 $$

$$ 3 \cos^2 x - 4 \cos x = 0 $$

Let $ t = \cos x $ to simplify the equation further:

$$ 3 t^2 - 4 t = 0 $$

This quadratic equation can be solved using the quadratic formula:

$$ t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Here, $ a = 3 $, $ b = -4 $, and $ c = 0 $:

$$ t = \frac{-(-4) \pm \sqrt{(-4)^2 - 4 \cdot 3 \cdot 0}}{2 \cdot 3} $$

$$ t = \frac{4 \pm \sqrt{16}}{6} $$

$$ t = \frac{4 \pm 4}{6} $$

So, the solutions to $ 3t^2 - 4t = 0 $ are:

$$ t = \begin{cases} t = \frac{4 + 4}{6} = \frac{8}{6} = \frac{4}{3} \\ \\ t = \frac{4 - 4}{6} = \frac{0}{6} = 0 \end{cases} $$

Note: Since $ c = 0 $, the solutions can also be found by factoring:

$$ 3 t^2 - 4 t = 0 $$

$$ t (3 t - 4) = 0 $$

This gives $ t = 0 $ or $ t = \frac{4}{3} $.

Since $ t = \cos x $:

$$ \cos x = \begin{cases} \frac{4}{3} \\ \\ 0 \end{cases} $$

However, $ \cos x = \frac{4}{3} $ is not possible because cosine values must lie within $[-1, 1]$. Thus, we discard this solution:

$$ \cos x = \frac{4}{3} = \nexists $$

The remaining solution, $ \cos x = 0 $, is valid:

$$ \cos x = 0 $$

To find $ x $, apply the inverse cosine function:

$$ \arccos(\cos x) = \arccos(0) $$

The inverse cosine of 0 is $ \pi/2 $ radians (90°):

$$ x = \arccos(0) = \frac{\pi}{2} $$

Since cosine is a periodic function with a period of $ \pi $ radians, the solutions are infinite:

$$ x = \frac{\pi}{2} + k \pi $$

Where $ k $ is any integer.

By varying $ k $ ($ k = 0, 1, -1, 2, -2, \ldots $), we can find all periodic solutions of the equation.

Thus, the solution to the original equation is $ x = \pi/2 $ plus any multiple of $ \pi $.

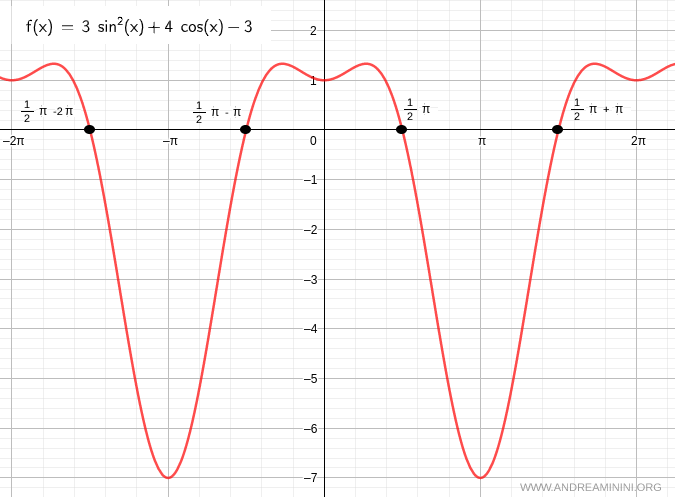
Graph of the equation

And so on.