How to Solve a Right Triangle Using Trigonometry

Solving a right triangle involves calculating the lengths of its sides and the measures of its angles based on the information provided.

To solve a right triangle, you need at least one of the following:

one side and one acute angle, or
two sides.

In either case, the Pythagorean theorem is a key tool.

A Practical Example

Different methods apply depending on the given data.

Example 1

You are given the lengths of both legs of a right triangle and need to calculate all the other elements.

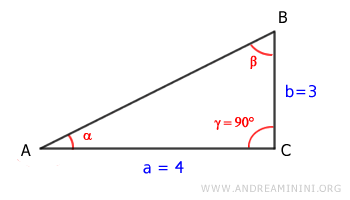
a right triangle with known leg lengths

The given side lengths are:

$$ a = 4 $$

$$ b = 3 $$

Using the Pythagorean theorem, we calculate the hypotenuse:

$$ c = \sqrt{a^2 + b^2} $$

$$ c = \sqrt{4^2 + 3^2} $$

$$ c = \sqrt{16 + 9} $$

$$ c = \sqrt{25} $$

$$ c = 5 $$

Thus, the hypotenuse is 5.

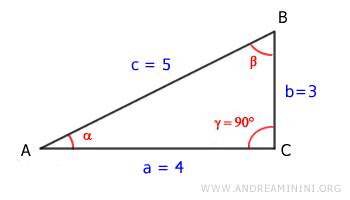
calculated hypotenuse length

Next, let’s determine the angles.

According to the fundamental trigonometric identity, tan α = sin α / cos α

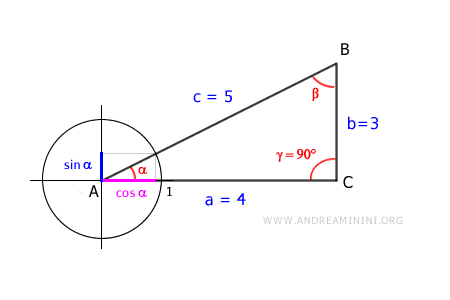
ratio of sine to cosine

The ratio sin α / cos α corresponds to the ratio of the sides b / a because they relate to the same angle α.

$$ \sin \alpha : \cos \alpha = b : a $$

We can therefore write:

$$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} = \frac{b}{a} $$

With the given leg lengths b = 3 and a = 4:

$$ \tan \alpha = \frac{3}{4} $$

To find α, apply the arctangent function to both sides:

$$ \arctan ( \tan \alpha ) = \arctan \left( \frac{3}{4} \right) $$

Since the arctangent is the inverse of the tangent function: arctan(tan α) = α

$$ \alpha = \arctan \left( \frac{3}{4} \right) $$

Now, calculate the arctangent of 3/4:

$$ \alpha = \arctan \left( \frac{3}{4} \right) = 36.87° $$

Note: For simplicity, angles in this exercise are expressed in degrees. However, remember that calculators often return the arctangent result in radians. If so, convert the result from radians to degrees if you prefer working in degrees.

At this point, we know α = 36.87° and γ = 90°.

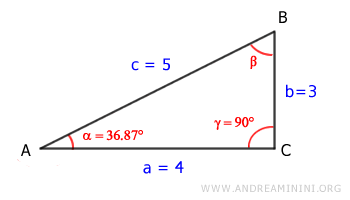
angle alpha is 36.87 degrees

Since the angles of a triangle always sum to 180° (or π radians):

$$ \alpha + \beta + \gamma = 180° $$

We calculate the remaining angle β as follows:

$$ \beta = 180° - \alpha - \gamma $$

$$ \beta = 180° - 36.87° - 90° = 53.13° $$

Thus, β = 53.13°.

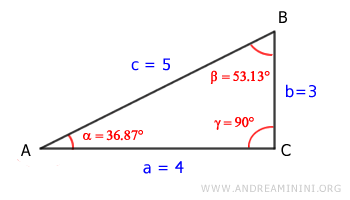
angle beta is 53.13 degrees

And that’s how you solve a right triangle.

This is the simplest scenario.

Example 2

In this example, we are given the length of the hypotenuse and one leg of the right triangle.

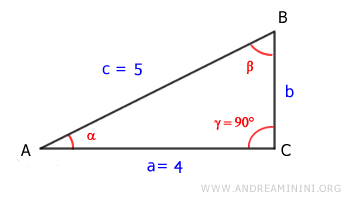
problem to solve

The known side lengths are:

$$ a = 4 $$

$$ c = 5 $$

To find the length of the other leg, there are two possible methods:

Method 1

Use the Pythagorean theorem:

$$ b = \sqrt{c^2 - a^2} $$

Proof: Since the hypotenuse is the square root of the sum of the squares of the two legs: $$ c = \sqrt{a^2 + b^2} $$ Square both sides of the equation: $$ c^2 = (\sqrt{a^2 + b^2})^2 $$ $$ c^2 = a^2 + b^2 $$ Rearrange the equation to isolate $ b $: $$ c^2 - a^2 = b^2 $$ Finally, take the square root of both sides: $$ \sqrt{c^2 - a^2} = \sqrt{b^2} $$ $$ b = \sqrt{c^2 - a^2} $$

Substituting $ c = 5 $ and $ a = 4 $:

$$ b = \sqrt{5^2 - 4^2} $$

$$ b = \sqrt{25 - 16} $$

$$ b = \sqrt{9} = 3 $$

Thus, the length of the other leg is $ b = 3 $.

Once the side lengths are known, the angles of the triangle can be calculated using the process described in the previous example.

Method 2

Alternatively, you can calculate the other leg using trigonometry, without applying the Pythagorean theorem.

According to the first theorem of right triangles:

$$ b = c \cdot \sin \alpha $$

$$ b = c \cdot \cos \beta $$

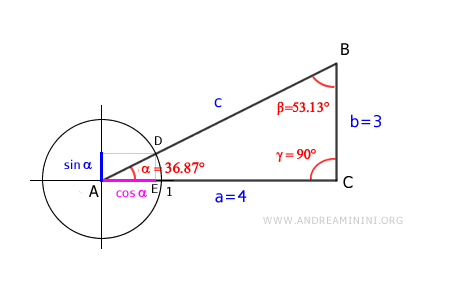
We draw the unit circle centered at vertex A.

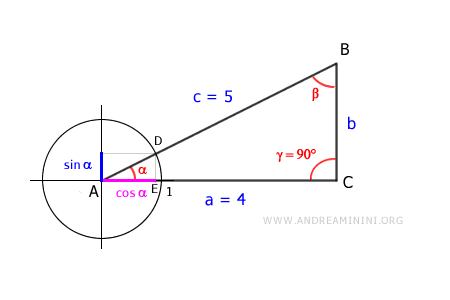
unit circle

Triangles ADE and ABC are similar because they share the same angles.

This leads to the following proportion:

$$ AE : AD = AC : AB $$

Here, $ AE $ represents $ \cos \alpha $:

$$ \cos \alpha : AD = AC : AB $$

The segment $ AC $ is the leg $ a = 4 $, and $ AB $ is the hypotenuse $ c = 5 $:

$$ \cos \alpha : AD = 4 : 5 $$

Since $ AD $ is the radius of the unit circle, $ AD = 1 $:

$$ \cos \alpha : 1 = 4 : 5 $$

Therefore, $ \cos \alpha $ is:

$$ \cos \alpha = \frac{4}{5} $$

Apply the arccosine function to find the angle:

$$ \arccos (\cos \alpha) = \arccos \left( \frac{4}{5} \right) $$

$$ \alpha = \arccos \left( \frac{4}{5} \right) $$

The arccosine of $ \frac{4}{5} $ is $ 36.87° $:

$$ \alpha = 36.87° $$

This gives us the angle $ \alpha = 36.87° $.

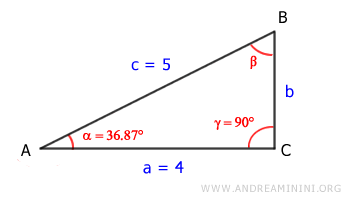
angle alpha is 36.87 degrees

With $ c = 5 $ and $ \alpha = 36.87° $, the length of leg $ b $ can be calculated using the sine of the opposite angle $ \alpha $:

$$ b = c \cdot \sin \alpha $$

$$ b = 5 \cdot \sin 36.87° $$

$$ b = 3 $$

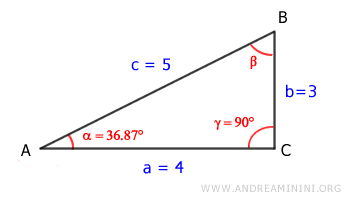
angle alpha is 36.87 degrees

Note: Alternatively, once the opposite angle $ \alpha = 36.87° $ is known, leg $ b $ can also be calculated using the cosine of the adjacent angle $ \beta $: $$ b = c \cdot \cos \beta $$ Since the angles of a right triangle sum to $ 180° $, the angle $ \beta $ can be found by subtraction: $$ \alpha + \beta + \gamma = 180° $$ $$ \beta = 180° - \alpha - \gamma $$ $$ \beta = 180° - 36.87° - 90° = 53.13° $$ Using this, the length of leg $ b $ is: $$ b = c \cdot \cos \beta $$ $$ b = 5 \cdot \cos 53.13° = 3 $$ This method is slightly longer but yields the same result.

Example 3

In this problem, we know the length of one leg ($ b $) and one acute angle ($ \alpha $) of a right triangle:

$$ b = 3 $$

$$ \alpha = 36.87^\circ $$

The task is to determine the remaining unknowns (angles and side lengths) of the triangle.

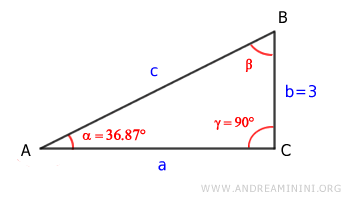
the problem

In a right triangle, the sum of the angles is always $ 180^\circ $:

$$ \alpha + \beta + \gamma = 180^\circ $$

Since two of the angles are already known, the third angle ($ \beta $) can be found by subtraction:

$$ 36.87^\circ + \beta + 90^\circ = 180^\circ $$

$$ \beta = 180^\circ - 36.87^\circ - 90^\circ = 53.13^\circ $$

Now all the angles of the triangle are known:

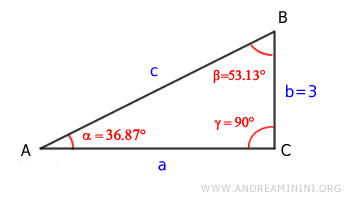
all angles are known

Next, let’s calculate the length of the other leg ($ a $) and the hypotenuse ($ c $). Using the unit circle centered at vertex $ A $:

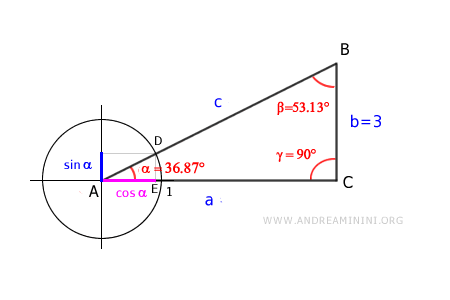
the unit circle

The triangles $ ADE $ and $ ABC $ are similar because they have the same angles.

This allows us to set up a proportion between their corresponding sides:

$$ \overline{AE} : \overline{DE} = \overline{AC} : \overline{BC} $$

Since $ \overline{BC} $ is the known leg $ b = 3 $:

$$ \overline{AE} : \overline{DE} = \overline{AC} : 3 $$

Here, $ \overline{AC} $ represents the leg $ a $:

$$ \cos \alpha : \sin \alpha = a : 3 $$

Rewriting the proportion as a fraction and solving for $ a $:

$$ a = 3 \cdot \frac{\cos \alpha}{\sin \alpha} $$

The ratio $ \frac{\cos \alpha}{\sin \alpha} $ is the cotangent of $ \alpha $:

$$ a = 3 \cdot \cot \alpha $$

With $ \alpha = 36.87^\circ $:

$$ a = 3 \cdot \cot 36.87^\circ $$

Using $ \cot 36.87^\circ = 1.33 $:

$$ a = 3 \cdot 1.33 = 4 $$

Thus, the other leg is $ a = 4 $.

Note: If your calculator lacks a cotangent function, you can use the identity $ \cot \alpha = \frac{1}{\tan \alpha} $: $$ a = 3 \cdot \frac{1}{\tan \alpha} $$ Alternatively, calculate the sine and cosine of $ \alpha $ separately. The final result will always be the same.

Next, let’s calculate the hypotenuse ($ c $).

With $ a = 4 $ and $ b = 3 $, the Pythagorean theorem gives:

$$ c = \sqrt{a^2 + b^2} = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 $$

However, for instructional purposes, we’ll also find $ c $ using trigonometry.

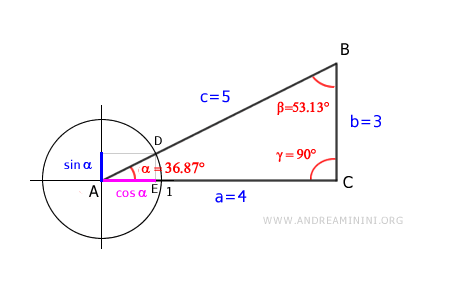
Returning to the similar triangles $ ABC $ and $ ADE $:

the length of leg a=4

Set up a proportion involving the hypotenuse and one of the legs:

$$ \overline{AD} : \overline{AE} = \overline{AB} : \overline{AC} $$

Here, $ \overline{AC} $ is the leg $ a = 4 $:

$$ \overline{AD} : \overline{AE} = \overline{c} : 4 $$

The segment $ \overline{AE} $ represents $ \cos \alpha $, and $ \overline{AD} $, the radius of the unit circle, equals $ 1 $:

$$ 1 : \cos \alpha = c : 4 $$

Rewriting the proportion as a fraction and solving for $ c $:

$$ c = \frac{4}{\cos \alpha} $$

Using $ \cos 36.87^\circ = 0.8 $:

$$ c = \frac{4}{0.8} = 5 $$

Thus, the hypotenuse is $ c = 5 $.

the hypotenuse c=5

Note: So far, I’ve provided detailed geometric and trigonometric explanations for each step. In practice, you can simply apply the formulas from the first theorem of right triangles.

Example 4

In this example, we know the length of the hypotenuse and one acute angle:

$$ c = 5 $$

$$ \beta = 53.13^\circ $$

Since this is a right triangle, we also know that one of the angles is a right angle: $ \gamma = 90^\circ $.

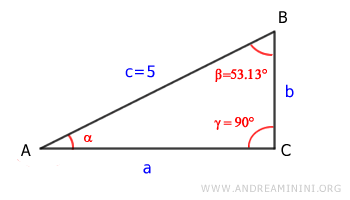
the problem to solve

The sum of the angles in any triangle is always $ 180^\circ $:

$$ \alpha + \beta + \gamma = 180^\circ $$

Substituting the known values:

$$ \alpha + 53.13^\circ + 90^\circ = 180^\circ $$

We can easily calculate $ \alpha $ by subtraction:

$$ \alpha = 180^\circ - 53.13^\circ - 90^\circ = 36.87^\circ $$

Now, we know the measures of all the angles:

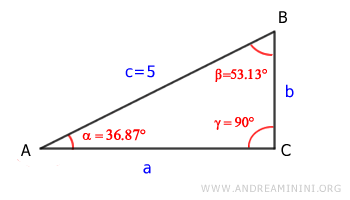
angle alpha is now known

To find the lengths of the legs, we use the first theorem of right triangles:

$$ a = c \cdot \cos \alpha $$

$$ b = c \cdot \sin \alpha $$

Here, we calculate both legs using the angle $ \alpha $:

The adjacent leg ($ a $) is determined using the cosine of $ \alpha $, while the opposite leg ($ b $) is found using the sine of $ \alpha $.

Note: Alternatively, you could use the angle $ \beta $, or a mix of both angles, to calculate the legs: $$ b = c \cdot \cos \beta $$ $$ a = c \cdot \sin \beta $$ Regardless of the method, the results will be the same.

Using $ c = 5 $ and $ \alpha = 36.87^\circ $, we calculate the lengths of the legs:

$$ a = 5 \cdot \cos 36.87^\circ = 4 $$

$$ b = 5 \cdot \sin 36.87^\circ = 3 $$

At this point, all side lengths and angle measures are known:

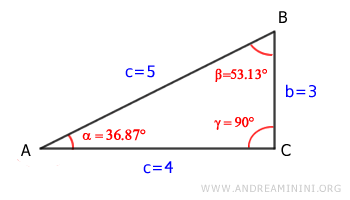
the triangle is solved

The triangle is now fully solved.

And that’s it!