Parametric Trigonometric Equations

A parametric trigonometric equation is a trigonometric equation, whether elementary or complex, that involves a real parameter $ k $. For example: $$ \cos x = 2k - 1 $$

The solutions to a parametric trigonometric equation depend on the specific value of $ k $.

As such, a parametric trigonometric equation may have a single solution for certain values of $ k $, multiple solutions, or no solution at all for others.

How to Approach a Parametric Trigonometric Equation

To analyze a parametric trigonometric equation, I study how its solutions vary as the parameter $ k $ changes.

A Practical Example

Let’s consider the following trigonometric equation:

$$ \begin{cases} 4 \cos 2x - k + 2 = 0 \\ \\ 0 \le x \le \frac{2}{3} \pi \end{cases} $$

This is an elementary trigonometric equation.

It is parametric because it includes a parameter $ k $, which can take any real value.

Moreover, the analysis of this equation is restricted to the interval $ x \in [0, 2\pi/3] $.

I first isolate the cosine function in the equation:

$$ \begin{cases} \cos 2x = \frac{k - 2}{4} \\ \\ 0 \le x \le \frac{2}{3} \pi \end{cases} $$

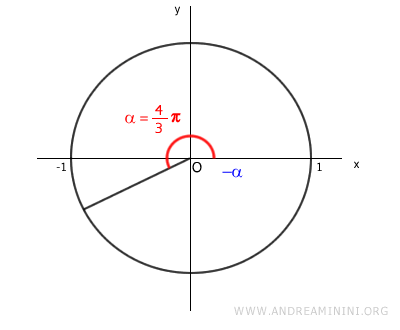
In the interval $ x \in [0, 2\pi/3] $, the argument (angle) of the function $ \cos 2x $ ranges from 0 to $ 4\pi/3 $ radians.

$$ 2x = \begin{cases} x = 0 \rightarrow \alpha = 2 \cdot 0 = 0 \\ \\ x = \frac{2}{3} \pi \rightarrow \alpha = 2 \cdot \frac{2}{3} \pi = \frac{4}{3} \pi = \pi + \frac{1}{3} \pi \end{cases}$$

Thus, the function $ \cos 2x $ takes values between -1 and 1 within the interval $ x \in [0, 4\pi/3] $.

analysis of the parametric trigonometric function

Next, I determine when the right-hand side, $(k-2)/4$, of the parametric equation falls within the interval [-1, 1].

$$ y = \frac{k - 2}{4} $$

This equation behaves as follows:

When $ k = 2 $, $ y = 0 $.
When $ k = 6 $, $ y = 1 $.
When $ k = -2 $, $ y = -1 $.
For $ k < -2 $ or $ k > 6 $, $ y $ lies outside the interval [-1, 1].

Hence, the parametric equation has at least one solution for $ k \in [-2, 6] $ and no solutions outside this range.

Next, I determine whether the equation has one or multiple solutions within $ k \in [-2, 6] $.

In the interval $ x \in [0, 4\pi/3] $, the function $ \cos 2x $ takes the same value twice when the argument (angle) lies between $ \pi - \pi/3 $ and $ \pi + \pi/3 $.

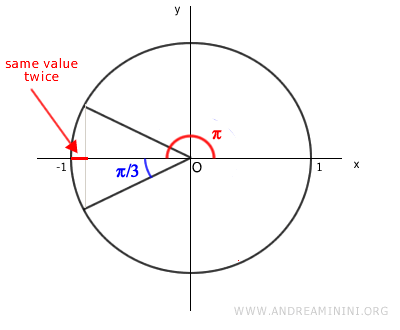
cosine function values repeat in an interval

I calculate the cosine value for $ \cos 4\pi/3 $.

I rewrite the argument $ 4\pi/3 $ in an equivalent algebraic form:

$$ \cos \frac{4}{3} \pi = \cos (\pi + \frac{1}{3} \pi) $$

Using the properties of associated angles for cosine:

$$ \cos (\pi + \frac{1}{3} \pi) = \cos (\pi - \frac{1}{3} \pi) $$

and:

$$ \cos (\pi - \frac{1}{3} \pi) = - \cos (\frac{1}{3} \pi) $$

This simplifies the calculation by bringing the angle into the first quadrant:

$$ \cos \frac{4}{3} \pi = - \cos (\frac{1}{3} \pi) $$

Knowing that the cosine of $ \pi/3 $ (60°) is $ 1/2 $:

$$ \cos \frac{4}{3} \pi = - \frac{1}{2} $$

Thus, the trigonometric equation has two solutions when $ \cos 2x \in [-1, -1/2] $ and a single solution when $ \cos 2x \in (-1/2, 1] $.

$$ \begin{cases} \cos 2x = \frac{k - 2}{4} \\ \\ 0 \le x \le \frac{2}{3} \pi \end{cases} $$

Now, I determine when the right-hand side of the parametric equation falls within the interval [-1, -1/2]:

$$ y = \frac{k - 2}{4} $$

The equation equals $ y = -1 $ when $ k = -2 $:

$$ -1 = \frac{k - 2}{4} $$

$$ -4 \cdot 1 + 2 = k $$

$$ k = -2 $$

The equation equals $ y = -1/2 $ when $ k = 0 $:

$$ -\frac{1}{2} = \frac{k - 2}{4} $$

$$ -4 \cdot \frac{1}{2} + 2 = k $$

$$ -2 + 2 = k $$

$$ k = 0 $$

Therefore, within the interval $ k \in [-2, 0] $, the equation has two solutions.

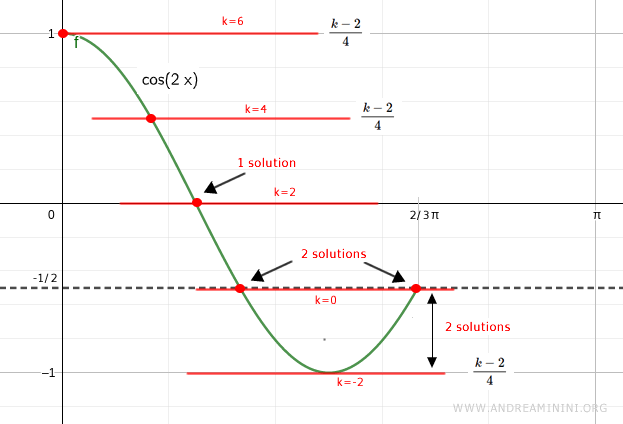
the parametric equation has two solutions for -2<k<0

Conversely, within the interval $ k \in (0, 6] $, the equation has only one solution.

For any other value $ k \notin [-2, 6] $, the equation has no solutions.

And so on.