Phase Angle in Trigonometry

In trigonometry, the phase angle is an angle that allows me to express a function $$ y = a \sin x + b \cos x $$ as an equivalent sinusoidal function $$ y = r \cdot \sin (x + k) $$

Here, k is the phase angle, and it is given by the arctangent of the ratio b/a.

$$ k = \arctan \frac{b}{a} $$

Meanwhile, r represents the amplitude of the sinusoid and is calculated as the square root of the sum of the squares of the coefficients, a²+b².

$$ r = \sqrt{a^2 + b^2} $$

Thus, a function like sin(x) + cos(x) can be rewritten as a sinusoid by applying a horizontal shift of k and a vertical scaling of r.

$$ y = a \sin x + b \cos x = r \cdot \sin (x + k) $$

Using the formulas for r and k, the complete transformation formula is:

$$ y = a \sin x + b \cos x = \sqrt{a^2 + b^2} \cdot \sin (x + \arctan \frac{b}{a}) $$

Note: When using the transformation formula, make sure to keep the signs of coefficients a and b consistent with those in the original function. For instance, if the original function is $$ y= \sin x - \cos x $$ the coefficients are $$ a=1$$ and $$ b=-1 $$

A Practical Example

Consider a function where a=2 and b=3:

$$ y=2 \sin x - 3 \cos x $$

The graph of this function is shown below:

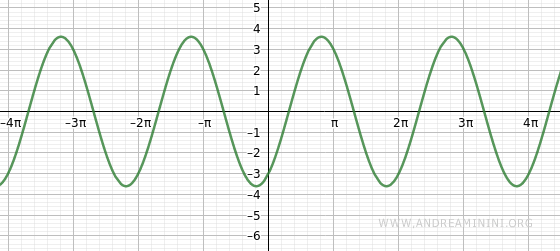
We want to express it in its equivalent form:

$$ y = r \sin (x + k) $$

The phase angle k is calculated as the arctangent of b/a:

$$ k = \arctan \frac{b}{a} = \arctan \frac{-3}{2} = -0.98 \ rad \ (approximately \ -56.3°) $$

The amplitude r is found as the square root of a²+b²:

$$ r = \sqrt{a^2+b^2} = \sqrt{2^2+3^2} = \sqrt{4+9} = \sqrt{13} $$

Therefore, the equivalent function is:

$$ y = \sqrt{13} \cdot \sin (x + (-0.98 \ rad )) $$

$$ y = \sqrt{13} \cdot \sin (x - 0.98 \ rad) $$

This results in a scaling of √13 and a shift of -0.98 radians (about -56.3°).

The graph of the transformed sinusoidal function matches the original one.

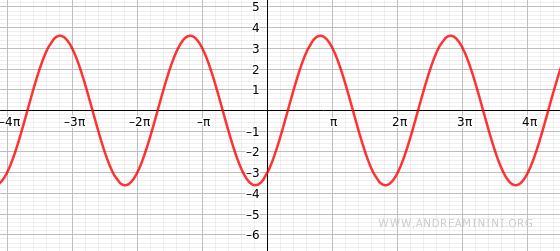
The Proof

The formula I want to demonstrate is a sinusoidal function:

$$ y = r \sin (x+k) $$

I apply the sine addition formula:

$$ y = r \cdot [ \sin x \cos k + \sin k \cos x ] $$

$$ y = r \sin x \cos k + r \sin k \cos x $$

I assign the two terms to the variables a and b:

$$ a = r \cos k $$

$$ b = r \sin k $$

This allows me to rewrite the function in its equivalent form:

$$ y = a \sin x + b \cos x $$

For this form to be equivalent, the coefficients a and b must satisfy the following system:

$$ \begin{cases} a = r \cos k \\ \\ b = r \sin k \end{cases} $$

I square both sides of each equation:

$$ \begin{cases} a^2 = r^2 \cos^2 k \\ \\ b^2 = r^2 \sin^2 k \end{cases} $$

I then add the equations together:

$$ a^2 + b^2 = r^2 \cos^2 k + r^2 \sin^2 k $$

$$ a^2 + b^2 = r^2 ( \cos^2 k + \sin^2 k ) $$

According to the Pythagorean identity, the sum of the squares of the cosine and sine is one: cos²+sin²=1

So, the equation simplifies to:

$$ a^2 + b^2 = r^2 $$

Taking the square root of both sides:

$$ \sqrt{a^2 + b^2} = \sqrt{r^2} $$

$$ \sqrt{a^2 + b^2} = r $$

Thus, I’ve determined the value of r, the amplitude of the sinusoid.

To find the angle k, I revisit the system of equations:

$$ \begin{cases} a = r \cos k \\ \\ b = r \sin k \end{cases} $$

Next, I divide both equations:

$$ \frac{b}{a} = \frac{r \sin k}{r \cos k} $$

$$ \frac{b}{a} = \frac{\sin k}{\cos k} $$

$$ \frac{b}{a} = \tan k $$

Applying the arctangent to both sides:

$$ \arctan \frac{b}{a} = \arctan \tan k $$

$$ \arctan \frac{b}{a} = k $$

Thus, I’ve also found the phase angle k of the sinusoid.

$$ k = \arctan \frac{b}{a} $$

And so forth.