Relationship Between the Slopes of Two Perpendicular Lines

When two lines are perpendicular, the slope of one line is the negative reciprocal of the slope of the other: $$ m_1 = - \frac{1}{m_2} $$

Here, m₁ represents the slope of one line:

$$ r_1: \ \ y = m_1 \cdot x + q $$

while m₂ represents the slope of the other line:

$$ r_2: \ \ y = m_2 \cdot x + q $$

A Practical Example

Let’s take two lines:

$$ r_1 : \ \ y = -4x + 2 $$

$$ r_2 : \ \ y = \frac{1}{4} \cdot x + 4 $$

Notice that the slopes of these lines are indeed negative reciprocals:

$$ m_1 = -4 $$ $$ m_2 = \frac{1}{4} $$

This confirms the perpendicularity condition:

$$ m_1 = - \frac{1}{m_2} $$

Thus, the two lines are perpendicular.

To verify this, I’ll graph them in GeoGebra and measure the angle at their intersection.

 

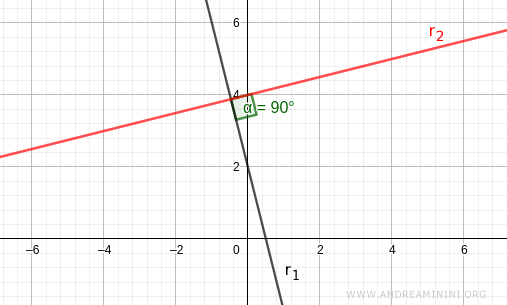
The intersection angle between these two lines is indeed a right angle of 90°.

The Proof

Consider two perpendicular lines, r₁ and r₂, intersecting at point P to form a 90° angle (π/2).

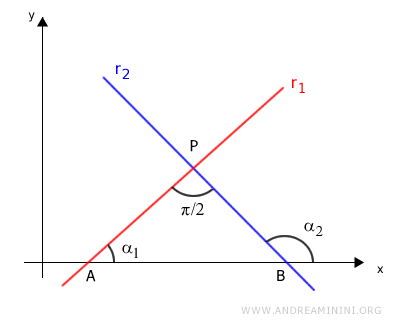
Line r₁ intersects the x-axis at point A, creating angle α₁, while line r₂ intersects it at point B, creating angle α₂.

Connecting points A, B, and P forms a right triangle, ABP.

In this triangle, we know the intersection angle is 90° (π/2), along with angle α₁.

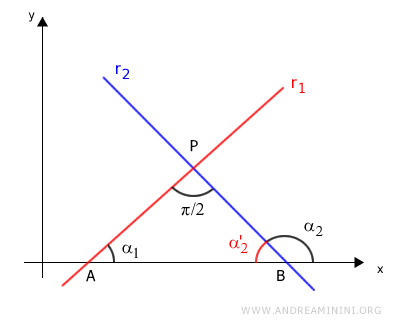
Angle α₂ is an exterior angle and a supplementary angle to the interior angle α₂'.

Since the sum of a triangle’s angles is always 180°, the supplementary angle α₂ equals the sum of the non-adjacent interior angles:

$$ a_2 = \frac{\pi}{2} + a_1 $$

Applying the tangent function (tan) to both sides, we get:

$$ \tan a_2 = \tan ( \frac{\pi}{2} + a_1 ) $$

Since the associated angle for tangent, tan(180°+x), equals -cot(x):

$$ \tan a_2 = -\cot(a_1) $$

Knowing that cotangent (cot) is the reciprocal of tangent:

$$ \tan a_2 = - \frac{1}{\tan(a_1)} $$

The tangent of angle α₂ gives the slope m₂ of one line, so tan α₂ = m₂:

$$ m_2 = - \frac{1}{\tan(a_1)} $$

The tangent of angle α₁ gives the slope m₁ of the other line, so tan α₁ = m₁:

$$ m_2 = - \frac{1}{m_2} $$

This completes the proof of the formula we set out to demonstrate.

And so on.