Solving Linear Equations with Sine and Cosine Using the Geometric Method
To solve a linear equation involving sine and cosine, you can apply the geometric (or graphical) method: $$ a \sin x + b \cos x + c = 0 $$
Start by creating a system that combines the linear trigonometric equation with the fundamental trigonometric identity:
$$ \begin{cases} a \sin x + b \cos x + c = 0 \\ \\ \cos^2 x + \sin^2 x = 1 \end{cases} $$
Next, replace sine and cosine with temporary variables, \( s = \sin x \) and \( t = \cos x \):
$$ \begin{cases} a \cdot s + b \cdot t + c = 0 \\ \\ s^2 + t^2 = 1 \end{cases} $$
Then, solve the system to find the values of \( s \) and \( t \).
These values represent a line on the plane, which may intersect the unit circle.
Once you have the values for sine and cosine, substitute them back into the system to determine the solutions for the trigonometric equation:
$$ \begin{cases} \cos x = s \\ \\ \sin x = t \end{cases} $$
A Practical Example
Let’s solve the linear equation:
$$ \sqrt{3} \sin x + \cos x = \sqrt{3} $$
Create a system using the fundamental trigonometric identity:
$$ \begin{cases} \sqrt{3} \sin x + \cos x = \sqrt{3} \\ \\ \cos^2 x + \sin^2 x = 1 \end{cases} $$
Substitute sine and cosine with \( s \) and \( t \):
$$ \begin{cases} \sqrt{3} s + t = \sqrt{3} \\ \\ t^2 + s^2 = 1 \end{cases} $$
Solve the system using substitution:
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ t^2 + s^2 = 1 \end{cases} $$
Expand and simplify:
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ (\sqrt{3} - \sqrt{3} s)^2 + s^2 = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ 3 - 2 \cdot 3 s + 4s^2 = 1 \end{cases} $$
This simplifies to the quadratic equation:
$$ 4s^2 - 6s + 2 = 0 $$
Solve it using the quadratic formula:
$$ s = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
$$ s = \frac{-(-6) \pm \sqrt{36 - 32}}{8} $$
$$ s = \frac{6 \pm 2}{8} $$
$$ s = \begin{cases} \frac{6 + 2}{8} = \frac{8}{8} = 1 \\ \\ \frac{6 - 2}{8} = \frac{4}{8} = \frac{1}{2} \end{cases} $$
The corresponding cosine values \( t = \cos x \) fall within the cosine’s valid range \([-1, 1]\).
Solution 1
If \( s = 1 \), then \( t = 0 \):
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ s = 1 \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} \cdot 1 \\ \\ s = 1 \end{cases} $$
$$ \begin{cases} t = 0 \\ \\ s = 1 \end{cases} $$
Since \( t = \cos x \) and \( s = \sin x \):
$$ \begin{cases} \cos x = 0 \\ \\ \sin x = 1 \end{cases} $$
The solution to this system is:
$$ x = \frac{\pi}{2} + 2 k \pi $$
Graphically, this corresponds to point C, at Cartesian coordinates \( (0,1) \), forming a 90° angle (\( \pi/2 \)).
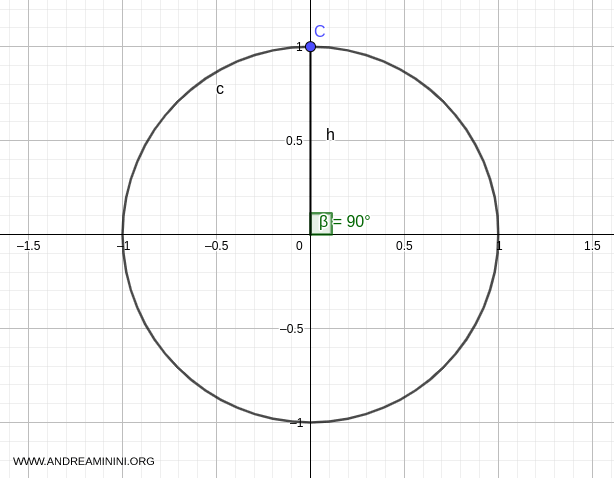
Substituting \( \alpha = \pi/2 \) into the general solution formula gives:
$$ x = \frac{\pi}{2} + 2 k \pi $$
By varying \( k \), you can find all solutions:
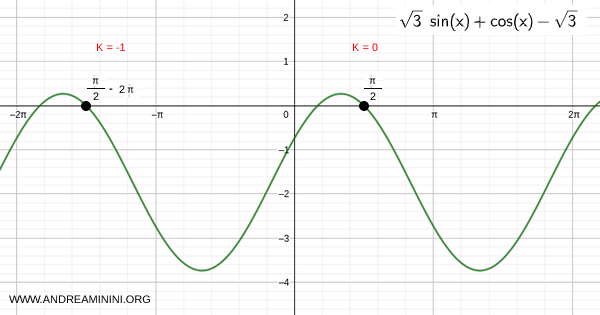
Solution 2
If \( s = \frac{1}{2} \), then \( t = \frac{\sqrt{3}}{2} \):
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} s \\ \\ s = \frac{1}{2} \end{cases} $$
$$ \begin{cases} t = \sqrt{3} - \sqrt{3} \cdot \frac{1}{2} \\ \\ s = \frac{1}{2} \end{cases} $$
$$ \begin{cases} t = \frac{\sqrt{3}}{2} \\ \\ s = \frac{1}{2} \end{cases} $$
Since \( t = \cos x \) and \( s = \sin x \):
$$ \begin{cases} \cos x = \frac{\sqrt{3}}{2} \\ \\ \sin x = \frac{1}{2} \end{cases} $$
The solution to this system is:
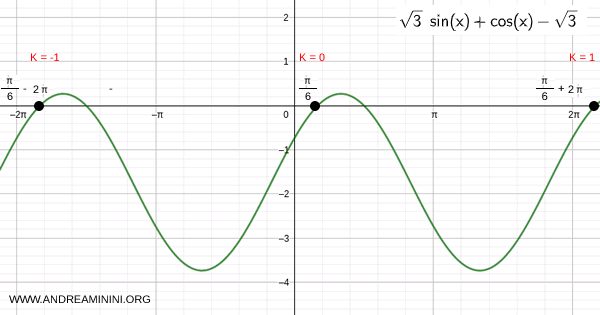
$$ x = \frac{\pi}{6} + 2 k \pi $$
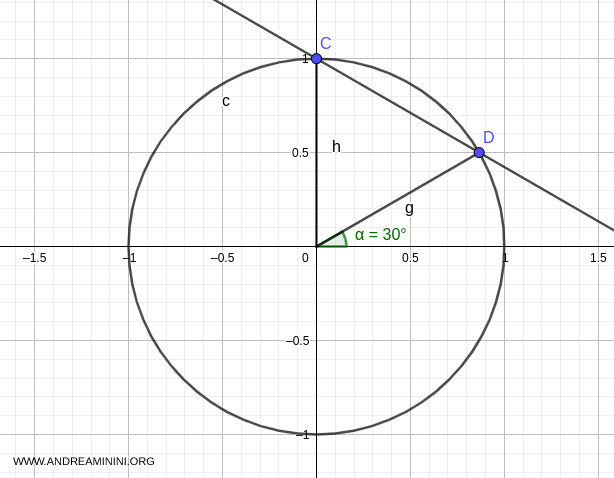
Graphically, this corresponds to point D, at Cartesian coordinates \( \left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right) \), forming a 30° angle (\( \pi/6 \)).
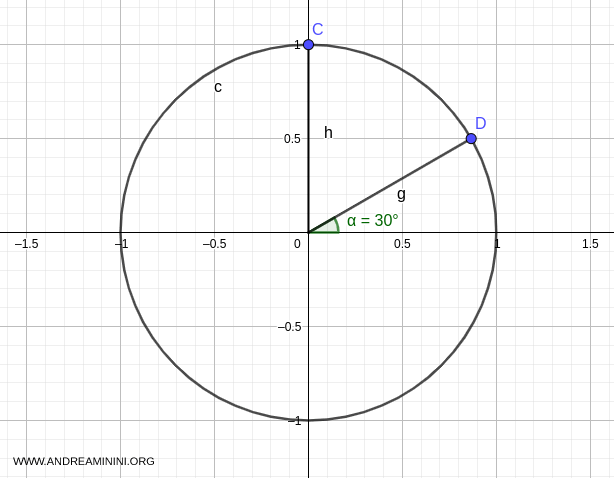
Substituting \( \alpha = \pi/6 \) into the general solution formula gives:
$$ x = \frac{\pi}{6} + 2 k \pi $$
By varying \( k \), you can find all solutions:
Conclusion
The solutions to the linear equation are:
$$ x = \frac{\pi}{2} + 2 k \pi \ \text{or} \ x = \frac{\pi}{6} + 2 k \pi $$
Here, \( k \) is any integer.
These two solutions correspond to points C and D, where the line intersects the unit circle at most twice.