Trigonometric Equation: sin x = c

The trigonometric equation $$ \sin x = c $$ is a basic trigonometric equation where x is the input for the sine function, and c is any real number.

This equation is defined only if the value of c falls within the range c ∈ [-1,1].

$$ -1 \le c \le 1 $$

If c lies outside the closed interval [-1,1], the equation has no solution because it does not match the sine function’s range.

Note: In trigonometry, the sine function only takes values between -1 and 1.

When the equation is defined, it has infinitely many solutions of the form α+2πk or π-α+2πk.

$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$

To solve the equation, I’ll find the angle α using the inverse sine function, also known as the arcsine.

$$ \arcsin c = \alpha $$

The arcsine function returns the angle α such that sin α = c.

A Practical Example

Let’s check if this trigonometric equation has solutions:

$$ \sin x = \frac{1}{2} $$

The equation is defined because the constant term is within the sine’s range.

$$ -1 \le \frac{1}{2} \le 1 $$

Therefore, the equation has the following solutions:

$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$

To find the angle α, I calculate the arcsine of 1/2, which equals π/6 (or 30°).

$$ \arcsin \frac{1}{2} = \frac{\pi}{6} $$

Next, I substitute the angle α = π/6 into the solution formula:

$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$

$$ x = \frac{\pi}{6} + 2\pi k \vee (\pi - \frac{\pi}{6}) + 2\pi k $$

Graphically, these solutions appear as follows:

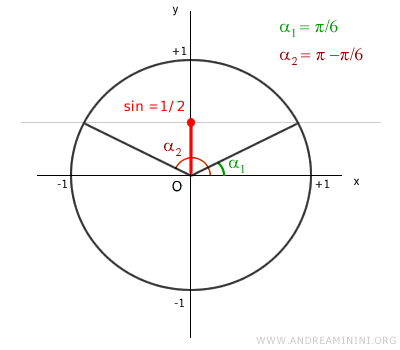
For both π/6 and π - π/6, the equation sin x = 1/2 holds true.

Because sine is a periodic function, we also include integer multiples k of a full circle, 2πk, in the solution set.

$$ x = \frac{\pi}{6} + 2\pi k \vee (\pi - \frac{\pi}{6}) + 2\pi k $$

Therefore, the equation sin x = 1/2 has infinitely many solutions of the form π/6 + 2πk and π - π/6 + 2πk.

The Proof

We begin by drawing the unit circle on the Cartesian plane.

The unit circle has a radius of 1.

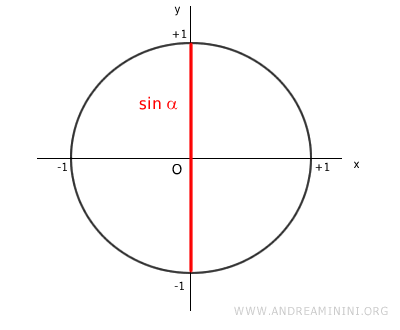
The sine function’s value is measured along the y-axis and ranges from -1 to +1 (the sine’s range).

Taking any real number c, let’s examine if the equation has solutions.

If the value of c exceeds 1, the line y=c is parallel to the x-axis and does not intersect the unit circle.

As a result, there is no angle x that gives a sine value greater than 1.

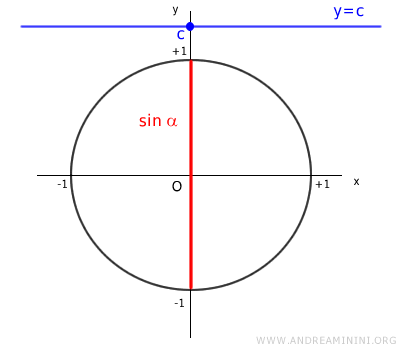
Similarly, if the value of c is less than -1, no angle x will yield the value c for sine.

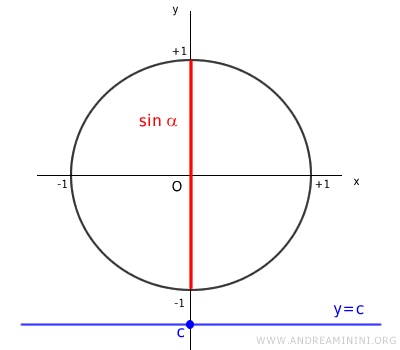
Therefore, the equation sin x = c is defined only if c lies within the interval [-1,1]

$$ -1 \le c \le 1 $$

Now, let’s consider a value of c within the interval [-1,1].

The equation y=c is a line parallel to the x-axis that intersects the unit circle at two points, P₁ and P₂.

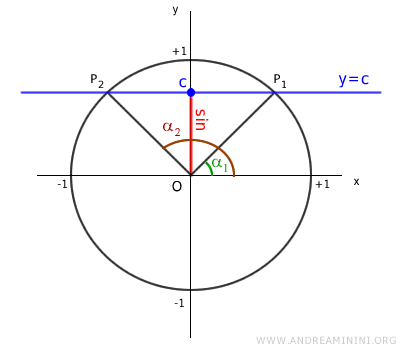
These points, P₁ and P₂, are endpoints of radii at angles α₁ and α₂.

Thus, for the value c, there are two angles α₁ and α₂ that satisfy the equation sin x = c.

$$ \sin \alpha_1 = \sin \alpha_2 = c $$

Both α₁ and α₂ solve the equation, so we can write:

$$ x = \alpha_1 \vee \alpha_2 $$

However, these aren’t the only possible solutions.

Sine is a periodic function that repeats its values every period of 2π.

We therefore include the sums of α₁ and α₂ with integer multiples of 2πk in the solution set.

$$ x = \alpha_1 + 2\pi k \vee \alpha_2 + 2\pi k $$

The angles α₁ and α₂ are associated angles for sine because they produce the same result, sin(α₁) = sin(α₂).

Thus, we can rewrite α₂ as π - α₁.

$$ x = \alpha_1 + 2\pi k \vee (\pi - \alpha_1) + 2\pi k $$

With only one angle α₁, we can simplify further by writing α = α₁.

$$ x = \alpha + 2\pi k \vee (\pi - \alpha) + 2\pi k $$

Thus, if c lies within the interval [-1,1], the equation sin x = c is defined and has infinitely many solutions of the form x = α+2πk or π-α+2πk.

$$ \sin x = c $$

Note: In cases where c = 1 or c = -1, the line y = c intersects the unit circle at only one point instead of two. The solution set includes these specific cases where $$ \alpha = \pi - \alpha $$

To find the angle α, I apply the arcsine function to both sides of the equation.

$$ \arcsin( \sin x ) = \arcsin c $$

The arcsine is the inverse of the sine function.

So, arcsin(sin x) = x

$$ x = \arcsin c $$

This way, I find the solution x to the trigonometric equation sin x = c.

And so on.