Trigonometric Equation: tan x = c

The equation $$ \tan x = c $$ is a basic trigonometric equation where the unknown x represents the argument of the tangent function, while c is any real number.

The equation tan x = c always has a solution and yields infinitely many solutions of the form α + kπ.

$$ x = \alpha + k \pi $$

Note: The equation tan x = c is defined for any value of c because the range of the tangent function ( -∞ , +∞ ) spans all real numbers.

To solve the equation, I find the angle α using the inverse tangent function, known as the arctangent.

$$ \arctan c = \alpha $$

The arctangent function returns the angle α such that tan α = c.

A Practical Example

Let’s check if this trigonometric equation has solutions:

$$ \tan x = 1 $$

This equation is always solvable for any real number and provides the following solutions:

$$ x = \alpha + k \pi $$

To find the angle α, I calculate the arctangent of 1, which is equal to π/4 (or 45°).

$$ \arctan 1 = \frac{\pi}{4} $$

I then substitute α = π/4 into the solution formula:

$$ x = \alpha + k \pi $$

$$ x = \frac{\pi}{4} + k \pi $$

Graphically, the solution looks like this:

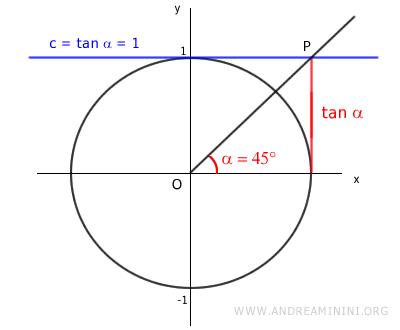
At an angle of π/4 radians (45°), the equation tan x = 1 is satisfied.

Since the tangent function is periodic, I also include integer multiples of π (kπ) among the possible solutions.

$$ x = \frac{\pi}{4} + k \pi $$

For instance, the equation tan x = 1 is also satisfied at π/4 + π radians (that is, 45° + 180°).

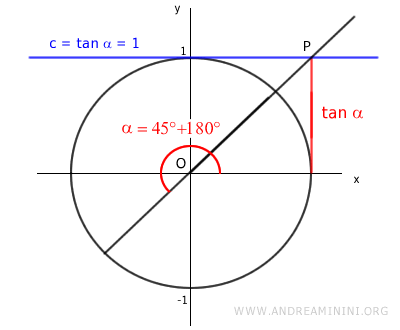
This pattern holds for any integer multiple of π, where k can be any positive or negative integer.

Thus, the trigonometric equation tan x = 1 has infinitely many solutions in the form π/4 + kπ.

The Proof

To illustrate this, let’s draw the unit circle on the Cartesian plane.

The unit circle is a circle with a radius of 1.

The value of the tangent function is represented along the vertical y-axis and ranges from -∞ to +∞ (the range of the tangent function).

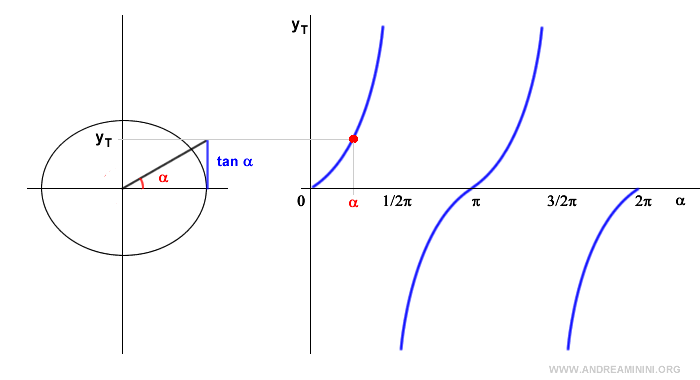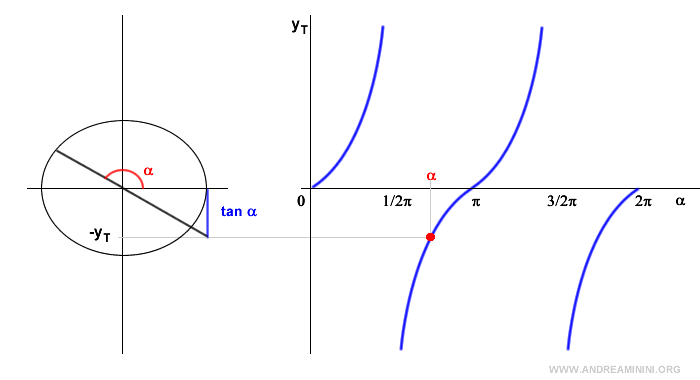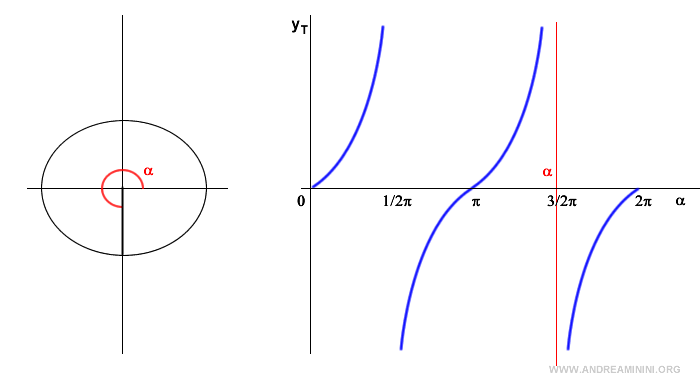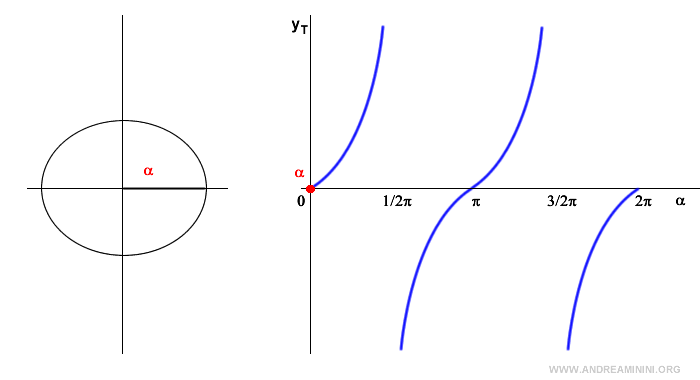
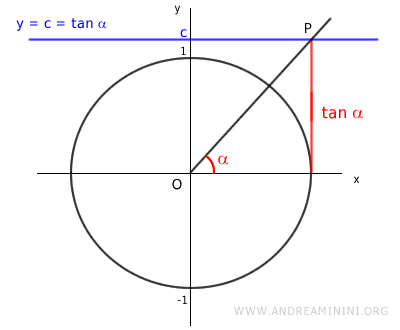
Now, let’s take any real value c and see if the trigonometric equation has solutions.

No matter the chosen value of c, whether positive or negative, the line y = c is a horizontal line that intersects the tangent function at a point P.

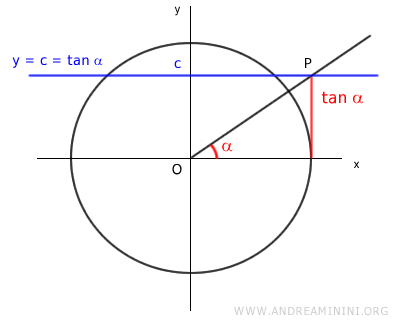
The tangent function is defined for values beyond the radius of the unit circle.

Thus, it can assume values greater than 1 and less than -1.

The trigonometric equation tan x = c is also defined for any negative value of c.

 

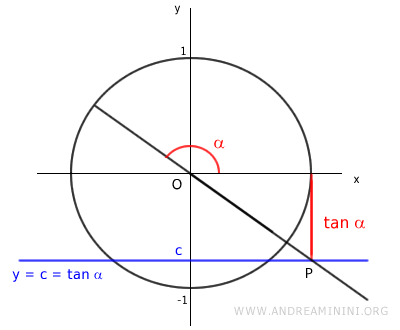
Therefore, there is no value of c for which the trigonometric equation tan x = c is undefined.

For any value of c, there is an angle α that satisfies the equation tan x = c

$$ \tan \alpha = c $$

However, this is not the only solution.

The tangent function is periodic with a period of π, meaning it repeats the same values.

So, in the set of solutions, I also consider the angle α plus integer multiples of π (kπ).

$$ x = \alpha + k \cdot \pi $$

How to find the angle?

To find α, I apply the arctangent function to both sides of the equation tan x = c:

$$ \arctan( \tan x ) = \arctan c $$

The arctangent is the inverse of the tangent function.

Therefore, arctan(tan x) = x

$$ x = \arctan c $$

This way, I find the angle x that corresponds to the value c = tan x.

And so on.