Trigonometric Equation: tan(a) = tan(b)

The trigonometric equation $$ \tan \alpha = \tan \alpha' $$ holds when the angles are congruent, meaning α = α' plus an integer multiple \( k \) of a half-turn angle, \( \pi \) radians (180°). The solutions to this equation are given by $$ \alpha = \alpha' + k \pi $$.

The tangent function is periodic, repeating every \( \pi \) radians.

So, this trigonometric equation has infinitely many solutions when considering integer multiples \( k \) of half a full turn, \( \pi \).

Here, \( k \) can be any integer in the range (-∞, ∞).

An Example

Let’s solve the trigonometric equation

$$ \tan \frac{1}{2}x = \tan 3x $$

The angles for the two tangent functions are:

$$ \alpha_1 = \frac{1}{2}x $$

$$ \alpha_2 = 3x $$

Using the trigonometric equation formula for \( \tan x = \tan y \):

$$ \alpha = \alpha' + k \pi $$

Substitute in α and α':

$$ \frac{1}{2}x = 3x + k \pi $$

Simplifying to isolate \( x \):

$$ \frac{1}{2}x - 3x = k \pi $$

$$ \frac{1-6}{2}x = k \pi $$

$$ -\frac{5}{2}x = k \pi $$

Now, multiply both sides by -1:

$$ -\frac{5}{2}x \cdot (-1) = k \pi \cdot (-1) $$

$$ \frac{5}{2}x = -k \pi $$

Then, multiply both sides by \( \frac{2}{5} \):

$$ \frac{5}{2}x \cdot \frac{2}{5} = -k \pi \cdot \frac{2}{5} $$

$$ x = -\frac{2}{5} \cdot k \pi $$

Now, to find solutions to the trigonometric equation, vary the integer constant \( k \).

Checking for k=0

$$ x = - \frac{2}{5} \cdot k \pi $$

$$ x = - \frac{2}{5} \cdot 0 \pi $$

$$ x = 0 $$

One solution to the trigonometric equation is the trivial solution x=0

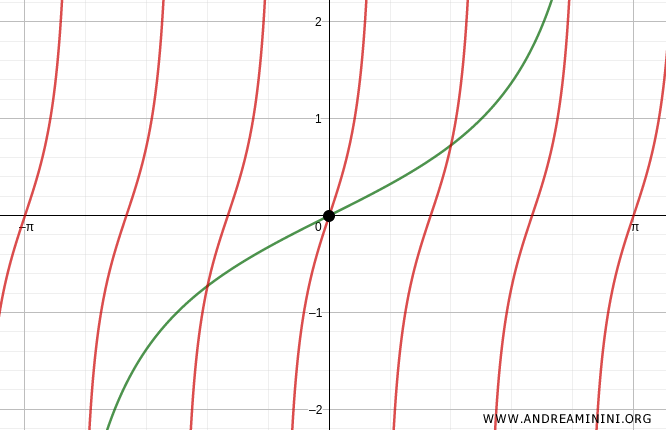
Checking for k=1

$$ x = - \frac{2}{5} \cdot k \pi $$

$$ x = - \frac{2}{5} \cdot 1 \pi $$

$$ x = - \frac{2}{5} \pi $$

Another solution to the trigonometric equation is x=-\frac{2}{5}\pi

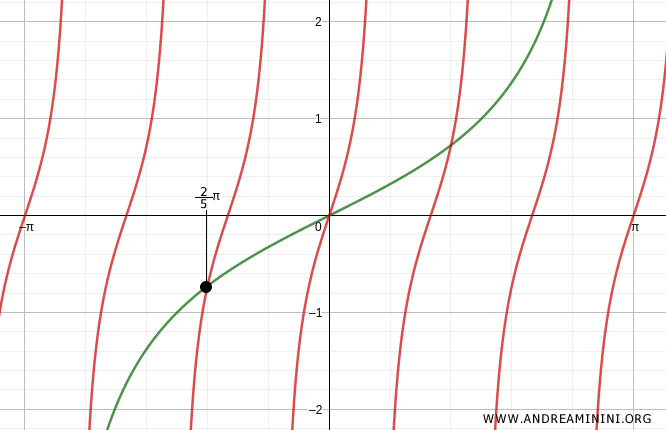
Checking for k=-1

$$ x = - \frac{2}{5} \cdot k \pi $$

$$ x = - \frac{2}{5} \cdot (-1) \pi $$

$$ x = \frac{2}{5} \pi $$

Another solution to the trigonometric equation is x=\frac{2}{5}\pi

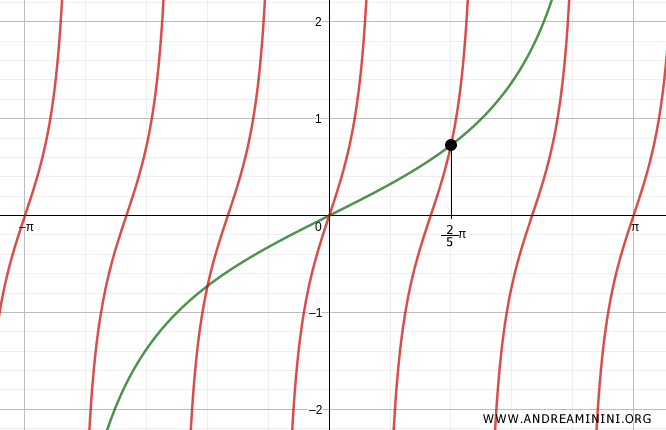
By continuing with \( k=2,3,... \), you can find infinitely many solutions to the trigonometric equation.

The Proof

Consider two angles α₁ and α₂ that yield the same tangent value \( c \):

$$ \tan \alpha_1 = \tan \alpha_2 = c $$

Two angles have the same tangent value under two conditions:

• when the angles are congruent (α₁=α₂)
• when the angles differ by an integer \( k \) multiple of \( \pi \): (α₁=α₂+kπ)

Since the tangent function is periodic with period \( \pi \), \( k \) can be any integer.

Graphically:

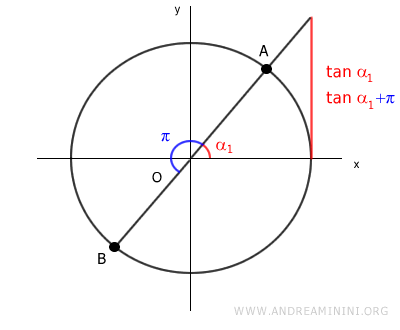
The second condition also includes the first when \( k=0 \).

$$ \alpha_1 = \alpha_2 \Leftrightarrow \alpha_1 = \alpha_2 + k \pi \quad \text{for} \quad k = 0 $$

Thus, the single necessary condition for the same tangent value is:

$$ \alpha_1 = \alpha_2 + k \pi $$

This confirms the formula for finding the solutions of a trigonometric equation of the form tan α₁ = tan α₂.

$$ \alpha_1 = \alpha_2 + k \pi $$

And so forth.