Trigonometric Function Values for 30° (π/6)

An angle of π/6 radians (pi over six) is equivalent to 30 degrees.

What are the sine and cosine of π/6 radians? What about the tangent and cotangent?

We can determine the trigonometric function values for an angle of π/6 through simple geometric reasoning.

Let’s start with a unit circle.

the unit circle

This is a circle with a radius of one, r=1.

I draw a segment OP forming an angle of π/6 radians with the x-axis.

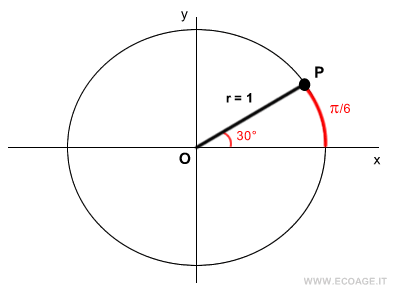
an angle of pi over six

I project the coordinates of point P onto the x-axis and y-axis.

This gives me two points, A and B, on the Cartesian plane.

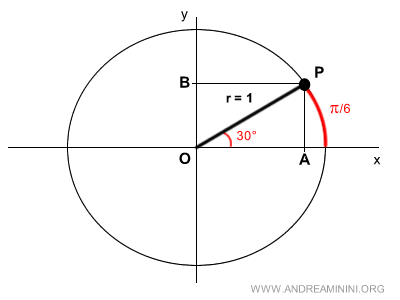
projection onto the axes

Connecting points O, P, and A forms a right triangle.

This right triangle has a right angle of π/2 (90°) and two complementary angles of π/3 radians (60°) and π/6 radians (30°).

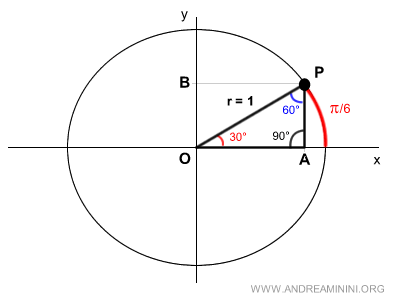
the triangle inscribed in the circle

Extending side PA, I find another point C on the unit circle.

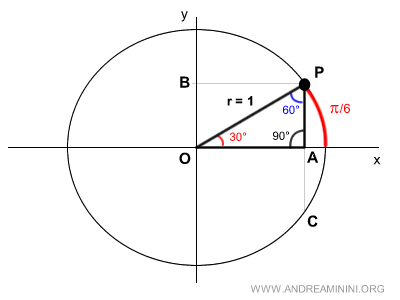
extension of side PA

This forms another right triangle, OAC, which is identical to the first one.

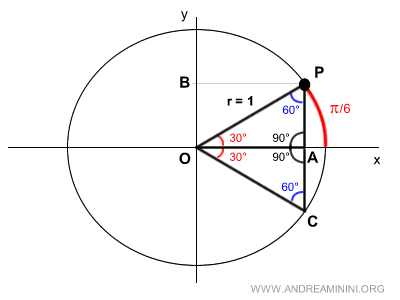
triangle OAC

By combining triangles OPA and OAC, we create triangle OPC.

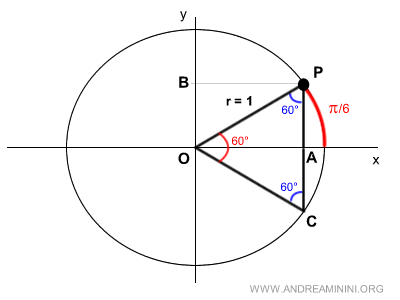
the union of the triangles

All angles in triangle OPC are equal to π/3 radians (60°).

Therefore, triangle OPC is an equilateral triangle.

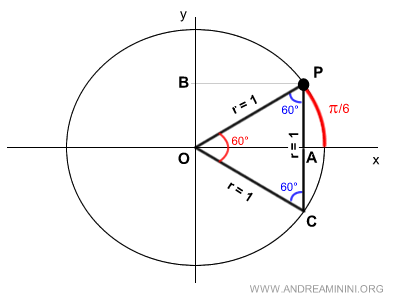
the equilateral triangle with sides of length 1

Since it’s inscribed in a unit circle, all the sides of the triangle are equal to the radius (r=1) of the circle.

$$ \overline{OP} = \overline{PC} = \overline{OC} = 1 $$

Knowing that segment PC is 1, we can find the length of segment PA, as it is half of PC.

$$ \overline{PA} = \frac{1}{2} \overline{PC} $$

$$ \overline{PA} = \frac{1}{2} \cdot 1 $$

$$ \overline{PA} = \frac{1}{2} $$

Segment PA represents the sine of the angle π/6.

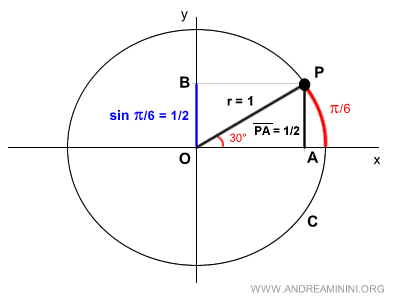
the sine of pi over six is one-half

Thus, we’ve found the sine of the angle π/6.

$$ \sin π/6 = \frac{1}{2} $$

Now that we know the length of one side, PA=1/2, and the hypotenuse, OP=1, in triangle OPA, we can use the Pythagorean theorem to find the missing side, OA.

$$ \overline{OA} = \sqrt{\overline{OP}^2- \overline{PA}^2 } $$

$$ \overline{OA} = \sqrt{1- \frac{1}{2}^2 } $$

$$ \overline{OA} = \sqrt{1- \frac{1}{4} } $$

$$ \overline{OA} = \sqrt{\frac{4-1}{4} } $$

$$ \overline{OA} = \sqrt{\frac{3}{4} } $$

$$ \overline{OA} = \frac{ \sqrt{3} } {2} $$

Segment OA represents the cosine of the angle π/6.

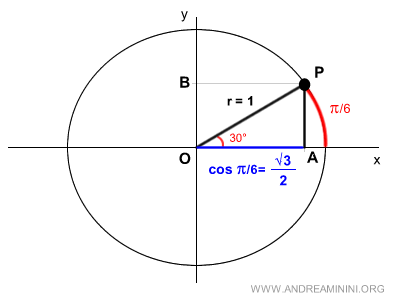
the cosine of pi over six

So, we’ve found the cosine of the angle π/6.

$$ \cos π/6 = \frac{ \sqrt{3} } {2} $$

With the sine and cosine values known, calculating the tangent of π/6 becomes straightforward.

$$ \tan π/6 = \frac{ \sin π/6 }{ \cos π/6 } $$

$$ \tan π/6 = \frac{ \frac{1}{2} }{ \frac{ \sqrt{3} } {2} } $$

$$ \tan π/6 =\frac{1}{2} \cdot \frac{ 2 } { \sqrt{3} } $$

$$ \tan π/6 =\frac{ 1} { \sqrt{3} } $$

To simplify, we multiply the numerator and denominator by the square root of 3.

$$ \tan π/6 =\frac{ 1} { \sqrt{3} } \cdot \frac{\sqrt{3}}{\sqrt{3} } = \frac{ \sqrt{3} }{ 3 } $$

In a similar way, we can determine the cotangent of π/6.

$$ cotg \ π/6 = \frac{ \cos π/6 }{ \sin π/6 } $$

$$ cotg \ π/6 = \frac{ \frac{ \sqrt{3} } {2} }{ \frac{1}{2} } $$

$$ cotg \ π/6 = \frac{ \sqrt{3} } {2} \cdot \frac{2}{1} $$

$$ cotg \ π/6 = \sqrt{3} $$

Using these simple geometric observations, we’ve calculated the trigonometric function values for a 30° angle (π/6).

And so on.