Trigonometric Inequality Systems
A trigonometric inequality system is made up of two or more trigonometric inequalities that share the same variable in their arguments. For example: $$ \begin{cases} 2 \sin x \leq 1 \\ \\ 2 \cos x < \sqrt{3} \end{cases} $$
How to Solve a Trigonometric Inequality System
To solve a system of trigonometric inequalities:
- Determine the solution for each individual trigonometric inequality.
- Check for any overlap between the solutions of the inequalities.
The solution to the system is the set of \(x\)-values that satisfy all the inequalities simultaneously.
A Practical Example
Let’s solve the following trigonometric inequality system:
$$ \begin{cases} 2 \sin x \leq 1 \\ \\ 2 \cos x < \sqrt{3} \end{cases} $$
First, we solve the first inequality:
$$ 2 \sin x \leq 1 $$
$$ \sin x \leq \frac{1}{2} $$
The basic equation \( \sin x = \frac{1}{2} \), related to this inequality, is satisfied when \(x\) takes the following values:
$$ x = \frac{\pi}{6} + 2k\pi \ \text{or} \ x = \pi - \frac{\pi}{6} + 2k\pi $$
$$ x = \frac{\pi}{6} + 2k\pi \ \text{or} \ x = \frac{6\pi - \pi}{6} + 2k\pi $$
$$ x = \frac{\pi}{6} + 2k\pi \ \text{or} \ x = \frac{5\pi}{6} + 2k\pi $$
Thus, within the interval \( (0, 2\pi) \), the inequality holds true in the intervals \([0, \pi/6]\) and \([5\pi/6, 2\pi)\).
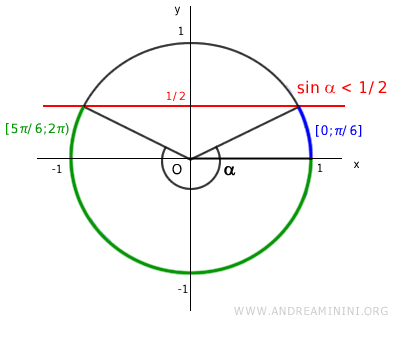
Next, we solve the second inequality:
$$ 2 \cos x < \sqrt{3} $$
$$ \cos x < \frac{\sqrt{3}}{2} $$
The basic equation \( \cos x = \frac{\sqrt{3}}{2} \), associated with this inequality, is satisfied when:
$$ x = \frac{\pi}{6} + 2k\pi \ \text{or} \ x = -\frac{\pi}{6} + 2k\pi $$
We rewrite \(-\pi/6\) in the reference interval \( (0, 2\pi) \) as \( 2\pi - \pi/6 \):
$$ x = \frac{\pi}{6} + 2k\pi \ \text{or} \ x = 2\pi - \frac{\pi}{6} + 2k\pi $$
$$ x = \frac{\pi}{6} + 2k\pi \ \text{or} \ x = \frac{12\pi - \pi}{6} + 2k\pi $$
$$ x = \frac{\pi}{6} + 2k\pi \ \text{or} \ x = \frac{11\pi}{6} + 2k\pi $$
Therefore, within the interval \( (0, 2\pi) \), the inequality holds true in the interval \( (\pi/6, 11\pi/6) \).
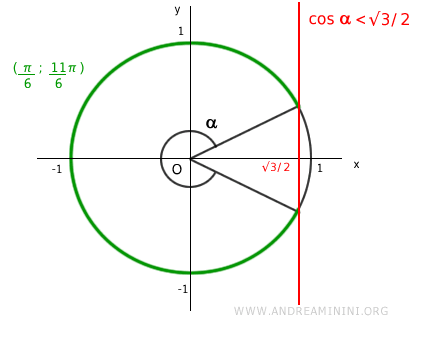
Finally, we check for an intersection between the solutions of the two inequalities:
$$ \{ [0, \frac{\pi}{6}] \ \cup \ [\frac{5\pi}{6}, 2\pi] \} \ \cap \ \{ (\frac{\pi}{6}, \frac{11\pi}{6}) \} $$
$$ [\frac{5\pi}{6}, \frac{11\pi}{6}) $$
An intersection exists, so the system has solutions.
In the interval \( (0, 2\pi) \), the solutions to the trigonometric inequality system are the \(x\)-values within \([5\pi/6, 11\pi/6)\).
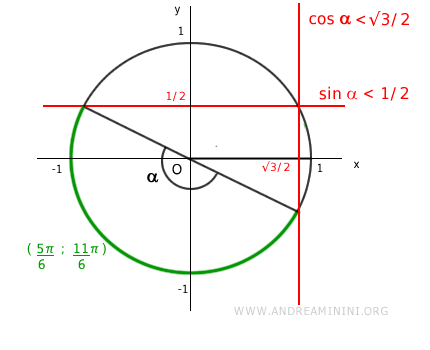
Considering all periodic solutions, the system is satisfied in the intervals:
$$ [\frac{5\pi}{6} + 2k\pi, \frac{11\pi}{6} + 2k\pi) $$
where \( k \) is any integer.
Verification with GeoGebra
To confirm the result, we analyze the graph of the two trigonometric functions over the interval \( (0, 2\pi) \).
Both functions are negative within the interval \( (5\pi/6, 11\pi/6) \).
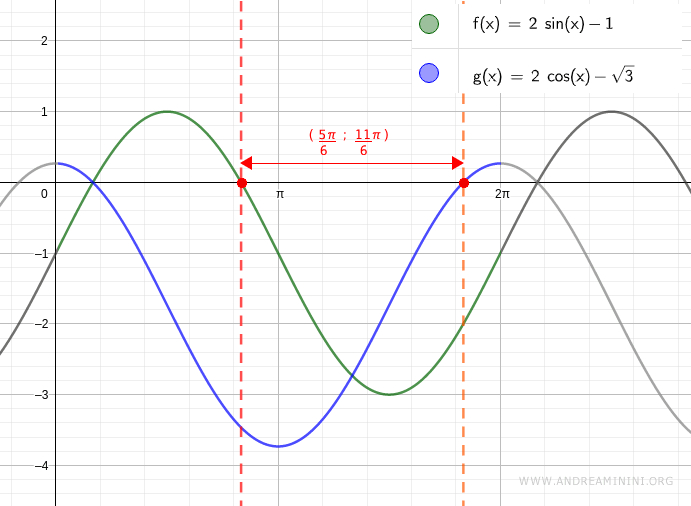
And so on.
