Values of Trigonometric Functions at 45° (π/4)

An angle of π/4 radians (pi over four) is equivalent to an angle of 45° degrees.

What are the sine and cosine values of π/4 radians? And what about the tangent and cotangent?

We can determine the trigonometric values for an angle of π/4 using simple geometric reasoning.

Let’s examine a unit circle.

The unit circle has a radius of 1 (r = 1).

We draw a line segment OP that makes an angle of π/4 radians with the x-axis.

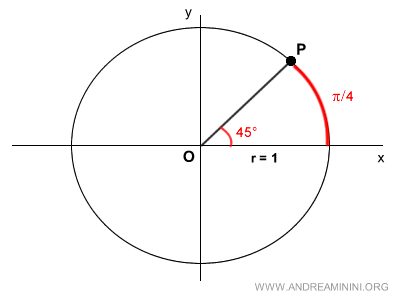
We then project the coordinates of point P onto the y-axis (vertical) and the x-axis (horizontal).

This gives us two points, A and B, on the coordinate plane.

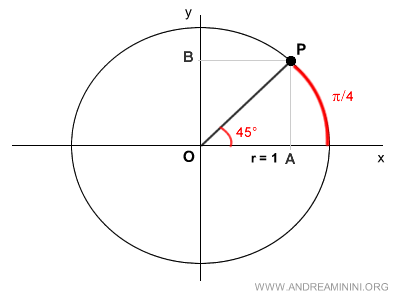
Connecting points O, P, and A forms a right triangle with a 90° angle and two equal angles of π/4 radians (45°).

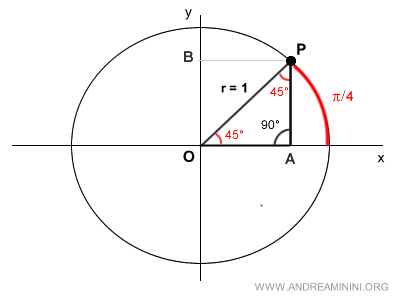
Since it has two equal angles (45°), it is also an isosceles triangle.

Therefore, the triangle has two equal sides, OA = PA, whose lengths are initially unknown.

$$ \overline{OA} = \overline{PA} $$

The length of side OP, however, is known as it is equal to the radius r = 1 of the unit circle.

$$ \overline{OP} = 1 $$

Applying the Pythagorean theorem:

$$ \overline{OA}^2 + \overline{PA}^2 = \overline{OP}^2 $$

Knowing that the hypotenuse is OP = 1:

$$ \overline{OA}^2 + \overline{PA}^2 = 1^2 $$

$$ \overline{OA}^2 + \overline{PA}^2 = 1 $$

Since the triangle is isosceles, OA and PA are equal.

We can substitute PA with OA in the equation:

$$ \overline{OA}^2 + \overline{OA}^2 = 1 $$

$$ 2 \overline{OA}^2 = 1 $$

Isolating OA:

$$ \overline{OA}^2 = \frac{1}{2} $$

Taking the square root of both sides:

$$ \sqrt{\overline{OA}^2} = \sqrt{\frac{1}{2}} $$

$$ \overline{OA} = \sqrt{\frac{1}{2}} $$

$$ \overline{OA} = \frac{1}{\sqrt{2}} $$

We rationalize the denominator:

$$ \overline{OA} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} $$

$$ \overline{OA} = \frac{\sqrt{2}}{2} $$

We have now found the length of OA, which corresponds to the cosine of 45° (π/4). 

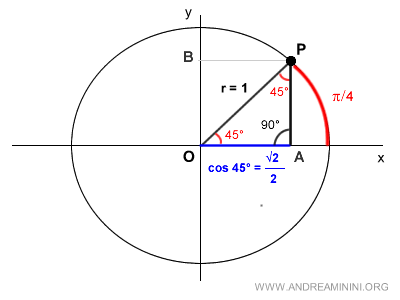
Thus, the cosine of the angle π/4 is:

$$ \cos \frac{\pi}{4} = \frac{\sqrt{2}}{2} $$

Since OA and PA have the same length in the isosceles triangle:

$$ \overline{PA} = \overline{OA} $$

$$ \overline{PA} = \frac{\sqrt{2}}{2} $$

Therefore, PA also represents the sine of 45° (π/4).

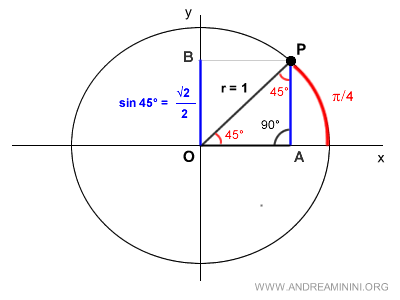
So, the sine of the angle π/4 is:

$$ \sin \frac{\pi}{4} = \frac{\sqrt{2}}{2} $$

With the values of sine and cosine known, we can calculate the tangent of π/4:

$$ \tan \frac{\pi}{4} = \frac{\sin \frac{\pi}{4}}{\cos \frac{\pi}{4}} $$

$$ \tan \frac{\pi}{4} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} $$

$$ \tan \frac{\pi}{4} = 1 $$

Finally, we find the cotangent of π/4:

$$ \cot \frac{\pi}{4} = \frac{\cos \frac{\pi}{4}}{\sin \frac{\pi}{4}} $$

$$ \cot \frac{\pi}{4} = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} $$

$$ \cot \frac{\pi}{4} = 1 $$

In this way, we’ve calculated the sine, cosine, tangent, and cotangent values for an angle of 45° (π/4) using simple geometric methods.

And so forth.