Area of a Circular Sector

You can calculate the area of a circular sector by knowing the radius (r) of the circle and the arc length (l) using the formula $$ Area_{sector} = \frac{l \cdot r}{2} $$ or, alternatively, by knowing the angle in radians (α) and the square of the radius (r²): $$ Area_{sector} = \frac{\alpha \cdot r^2}{2} $$

Practical Example

Let’s consider a circle with a radius of r=3 and a sector with an angle of α=28.44°.

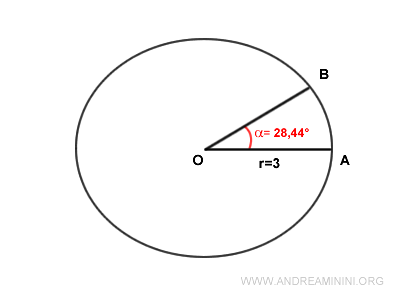
The first step is to convert the angle to radians.

$$ \alpha = 28.44° \cdot \frac{ \pi }{180°} = 0.5 \ rad $$

Important. It’s crucial to use the angle in radians. Keeping the angle in degrees is a serious mistake that will invalidate all calculations.

Once you have the angle in radians, you can easily calculate the arc length AB of the sector.

$$ AB = \alpha \cdot r $$

$$ AB = 0.5 \ rad \ \cdot 3 =1.5 \ $$

So, the arc length is l=1.5.

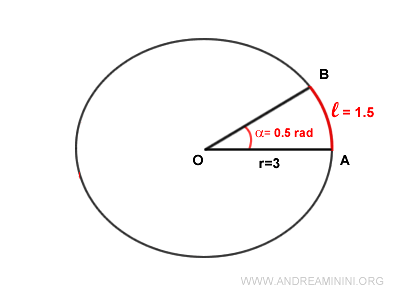
Now that we know the arc length (l=1.5) and the radius (r=3), we can calculate the area of the sector.

$$ A_{s} = \frac{l \cdot r}{2} $$

$$ A_{s} = \frac{1.5 \cdot 3}{2} = 2.25 $$

Therefore, the area of the sector is 2.25.

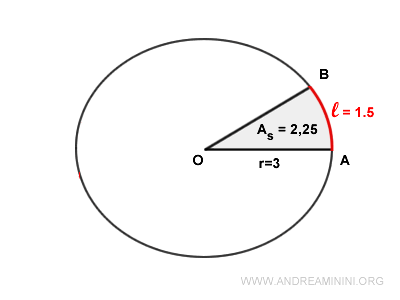
Note. You could also get the same result using the second formula once the angle is converted to radians and the radius is known: $$ A_{s} = \frac{\alpha \cdot r^2}{2} = \frac{ 0.5 \ \cdot 3^2 }{2} = \frac{ 4.5 }{2} = 2.25 $$

The Derivation

The formula for the area of a circular sector can be derived through a simple proportion.

The area of the sector relates to the area of the entire circle in the same way the angle relates to the full angle of the circle in radians (2π).

$$ Area_{sector} \ : \ Area_{circle} = \alpha \ : \ 2 \pi $$

In other words,

$$ \frac{ Area_{sector} }{ Area_{circle} } = \frac{ \alpha } { 2 \pi } $$

Now, isolating the area of the sector:

$$ Area_{sector} = \frac{ \alpha } { 2 \pi } \cdot Area_{circle} $$

Since the area of a circle is π·r²:

$$ Area_{sector} = \frac{ \alpha } { 2 \pi } \cdot \pi r^2 $$

We can cancel out π, which gives us the second formula.

$$ Area_{sector} = \frac{ \alpha } { 2 } \cdot r^2 $$

Now, express the angle as the ratio of the arc length to the radius (l/r).

$$ Area_{sector} = \frac{ 1 } { 2 } \cdot \frac{ l }{ r } \cdot r^2 $$

Canceling the radius (r), we get:

$$ Area_{sector} = \frac{ 1 } { 2 } \cdot l \cdot r $$

And this gives us the first formula as well:

$$ Area_{sector} = \frac{ l \cdot r } { 2 } $$

Thus, both formulas are now proven.

And that’s it.