Calculating the Angle Between Two Lines
Two lines, r and r', intersecting at a point on the plane $$ y = m \cdot x + q \\ y' = m' \cdot x' + q' $$ form an angle γ, which is given by the arctangent of the following ratio: $$ \gamma = \arctan \frac{m - m'}{1 + m \cdot m'} $$
where m and m' are the slopes of the respective lines.
A Practical Example
Consider the following two lines:
$$ r: \ \ \ y = 4x - 3 $$
$$ r': \ \ \ y = -x + 3 $$
We can calculate the angle between these intersecting lines using the formula:
$$ \gamma = \arctan \frac{m - m'}{1 + m \cdot m'} $$
The slope of the first line is m = 4, and the slope of the second line is m' = -1.
$$ \gamma = \arctan \frac{4 - (-1)}{1 + 4 \cdot (-1)} $$
$$ \gamma = \arctan \frac{5}{-3} $$
$$ \gamma = -59.03° $$
$$ \gamma = 59.03° $$
Here is a visual representation:
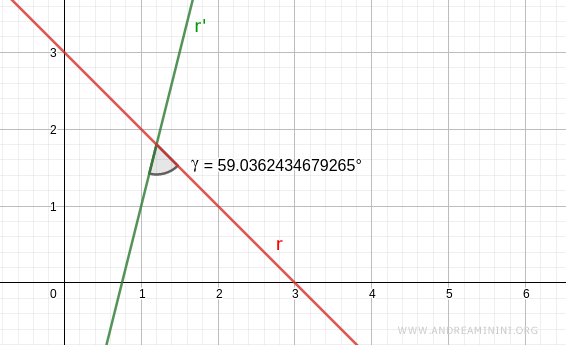
The other angle between the lines is supplementary.
It can be found by subtracting γ from 180° (π radians):
$$ \gamma' = \pi - \gamma $$
$$ \gamma' = 180° - 59.03° $$
$$ \gamma' = 120.96° $$
This is illustrated below:
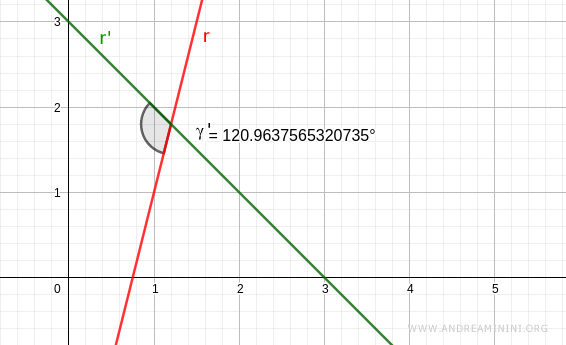
Note: The remaining two angles at the intersection are vertical angles, and therefore are equal to the angles we have calculated.
Example 2
Now consider two different intersecting lines, r and r':
$$ r: \ \ \ y = 3x - 2 $$
$$ r': \ \ \ y = x + 4 $$
Let's calculate the angle between them using the same formula:
$$ \gamma = \arctan \frac{m - m'}{1 + m \cdot m'} $$
The slope of the first line is m = 3, while the slope of the second line is m' = 1.
$$ \gamma = \arctan \frac{3 - (1)}{1 + 3 \cdot 1} $$
$$ \gamma = \arctan \frac{2}{4} $$
$$ \gamma = \arctan \frac{1}{2} $$
$$ \gamma = 26.56° $$
This is represented visually here:
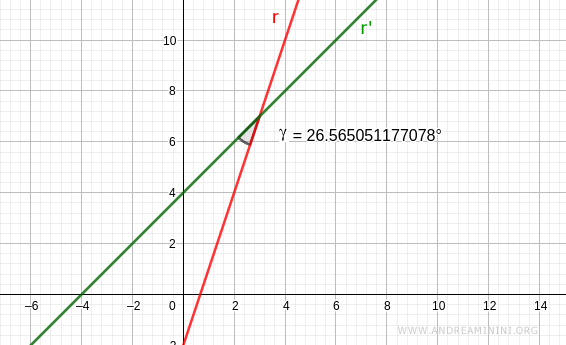
The other angle is supplementary.
Subtracting γ from 180° (π radians) gives us:
$$ \gamma' = \pi - \gamma $$
$$ \gamma' = 180° - 26.56° $$
$$ \gamma' = 153.43° $$
Graphically represented:
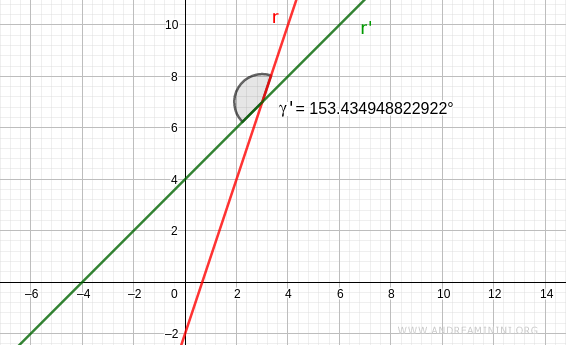
Note: The remaining two angles at the intersection are vertical angles and are therefore equal to those just calculated.
The Proof
Trigonometry is helpful for calculating the angle between two lines.
Two intersecting (non-parallel) lines, r and r', meet at a point P on the plane:
$$ r: \ \ y = m \cdot x + q $$ $$ r' : \ \ y' = m' \cdot x' + q' $$
where m and m' are the slopes of the lines.
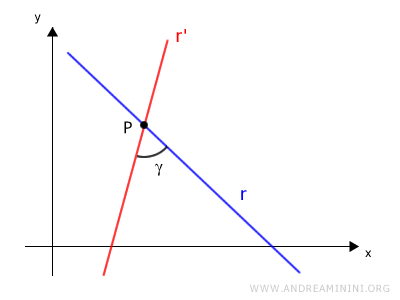
The lines intersect the x-axis at points A and B, forming angles α and β with the x-axis.
$$ \alpha = \tan \frac{y}{x} = m $$
$$ \beta = \tan \frac{y'}{x'} = m' $$
The points A, B, and P joined by line segments form the triangle ABP.
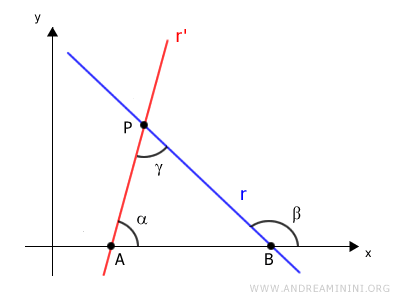
The internal angles of a triangle add up to π radians (180°).
The angle β is an external angle and equals the sum of the opposite internal angles, α and γ, as it supplements the interior angle β'.
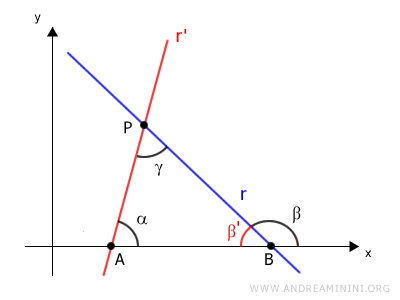
This allows us to write:
$$ \beta = \alpha + \gamma $$
Isolating γ gives:
$$ \gamma = \beta - \alpha $$
Taking the tangent of both sides, we have:
$$ \tan \gamma = \tan (\beta - \alpha) $$
Applying the tangent subtraction formula to the right side:
$$ \tan \gamma = \frac{\tan \beta - \tan \alpha}{1 + \tan \beta \cdot \tan \alpha} $$
Since the tangent of angle α is the slope m of the first line, tan α = m:
$$ \tan \gamma = \frac{\tan \beta - m}{1 + \tan \beta \cdot m} $$
And the tangent of angle β is the slope m' of the second line, tan β = m':
$$ \tan \gamma = \frac{m' - m}{1 + m' \cdot m} $$
If the tangent value is positive, the angle is acute; if negative, the angle is obtuse.
Taking the arctangent of both sides, we find the angle γ, which is the angle between the two lines:
$$ \arctan \tan \gamma = \arctan \frac{m' - m}{1 + m' \cdot m} $$
$$ \gamma = \arctan \frac{m' - m}{1 + m' \cdot m} $$
We've now derived the desired formula.
Note: In this proof, m' appears before m simply because, in this case, the angle is measured counterclockwise starting with line r'. This is simply a naming convention; the logic remains unchanged.
And so forth.
