Calculating Triangle Area Using Trigonometry

The area of a triangle is equal to half the product of two sides, l₁ and l_{2>, multiplied by the sine of the angle (α) between them. $$ Area = \frac{1}{2} \cdot (l_1 \cdot l_2) \cdot \sin \alpha $$}

In this formula, l₁ and l₂ represent two adjacent sides of the triangle, and α is the included angle.

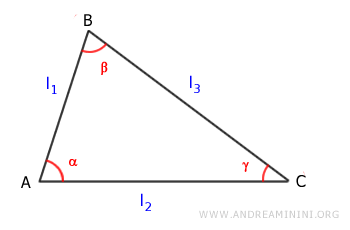
The following variations of the formula are also valid:

$$ Area = \frac{1}{2} \cdot (l_1 \cdot l_3) \cdot \sin \beta $$

$$ Area = \frac{1}{2} \cdot (l_2 \cdot l_3) \cdot \sin \gamma $$

These formulas apply to all types of triangles, whether isosceles, right, or scalene.

A Practical Example

Let’s start with a right triangle:

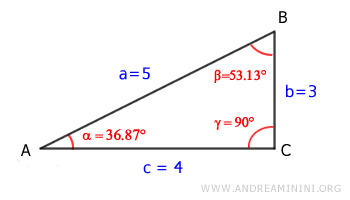
The area can be calculated as the base (c) multiplied by the height (b), divided by two:

$$ Area = \frac{1}{2} (c \cdot b ) = \frac{1}{2} (4 \cdot 3 ) = 6 $$

Now, let’s calculate the area using trigonometry.

Consider the adjacent sides, a = 5 and c = 4, and the included angle α = 36.87°.

$$ Area = \frac{1}{2} (a \cdot c ) \sin \alpha $$

$$ Area = \frac{1}{2} (5 \cdot 4 ) \sin 36.87° $$

$$ Area = \frac{1}{2} (20 ) \cdot 0.6 $$

$$ Area = 6 $$

The result is the same.

Similarly, using sides a = 5, b = 3, and the angle β = 53.13°, we get:

$$ Area = \frac{1}{2} (a \cdot b ) \sin \beta $$

$$ Area = \frac{1}{2} (5 \cdot 3 ) \sin 53.13° $$

$$ Area = \frac{1}{2} (15 ) \cdot 0.8 $$

$$ Area = 6 $$

Likewise, using sides c = 4, b = 3, and the angle γ = 90°, the result remains consistent:

$$ Area = \frac{1}{2} (c \cdot b ) \sin \gamma $$

$$ Area = \frac{1}{2} (4 \cdot 3 ) \sin 90° $$

$$ Area = \frac{1}{2} (12) \cdot 1 $$

$$ Area = 6 $$

No matter the approach, the area of the triangle is 6.

Example 2

Now, let’s consider an isosceles triangle:

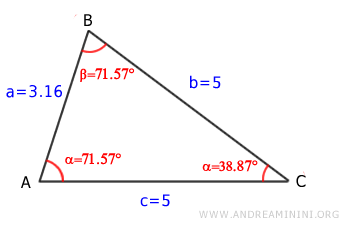
We calculate the area using sides b = 5, c = 5, and the included angle γ = 36.87°:

$$ Area = \frac{1}{2} (b \cdot c ) \sin \gamma $$

$$ Area = \frac{1}{2} (5 \cdot 5 ) \sin 36.87° $$

$$ Area = \frac{1}{2} (25 ) \cdot 0.6 $$

$$ Area = 7.5 $$

Alternatively, using sides a = 3.16 and c = 5 with the included angle α = 71.57°, we find:

$$ Area = \frac{1}{2} (a \cdot c ) \sin \alpha $$

$$ Area = \frac{1}{2} (3.16 \cdot 5 ) \sin 71.57° $$

$$ Area = 7.5 $$

Finally, using sides a = 3.16, b = 5, and the included angle β = 71.57°:

$$ Area = \frac{1}{2} (a \cdot b ) \sin \beta $$

$$ Area = 7.5 $$

Regardless of the calculation method, the result remains consistent.

The triangle’s area is 7.5.

The Proof

Case 1

Let’s begin with a right triangle:

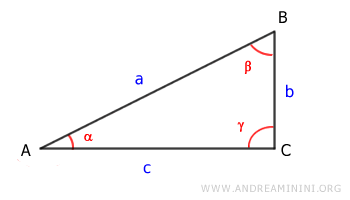
The area of the triangle can be calculated as the base (c) multiplied by the height (b), divided by two:

$$ Area = \frac{1}{2} \cdot c \cdot b $$

According to the First Theorem of Right Triangles, the height (b) is equal to the hypotenuse (a) multiplied by the sine of the opposite angle (α), expressed as b = a \cdot \sin α.

$$ Area = \frac{1}{2} \cdot c \cdot (a \cdot \sin \alpha) $$

$$ Area = \frac{1}{2} \cdot (c \cdot a) \cdot \sin \alpha $$

In this case, α is the angle between sides a and c of the triangle.

This confirms the formula.

Case 2

Next, let’s consider an isosceles triangle with sides b = c and angles α = β:

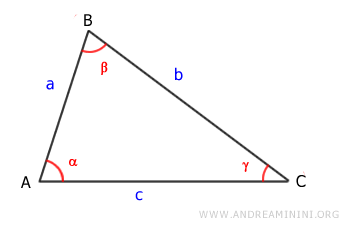
Draw the height (h) of the triangle, represented by segment BD:

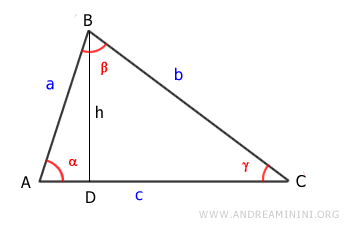
The area of the triangle can be calculated as the base (c) multiplied by the height (h), divided by two:

$$ Area = \frac{1}{2} \cdot c \cdot h $$

The height (h) corresponds to one leg of the right triangle ABD.

According to the First Theorem of Right Triangles, the length of segment BD (h) is equal to the hypotenuse (AB) multiplied by the sine of the opposite angle (α), expressed as h = a \cdot \sin α.

$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin \alpha $$

Here, α is the acute angle between sides a and c of the isosceles triangle.

This again validates the formula.

Case 3

Finally, let’s consider a scalene triangle with an obtuse angle (α):

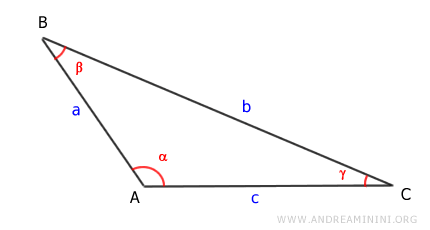
Draw the height (h) of the triangle, represented by segment AD:

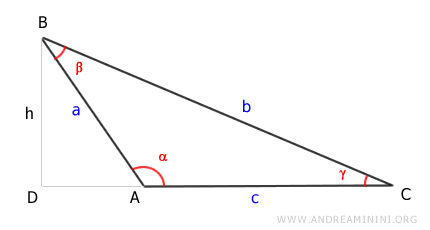
The area of the triangle is calculated as the base (c) multiplied by the height (h), divided by two:

$$ Area = \frac{1}{2} \cdot c \cdot h $$

Here, the height (h) is the length of segment AD in the right triangle ADB.

According to the First Theorem of Right Triangles, the height (h) is equal to the hypotenuse (AB) multiplied by the sine of the supplementary angle (π - α), expressed as h = a \cdot \sin(\pi - \alpha).

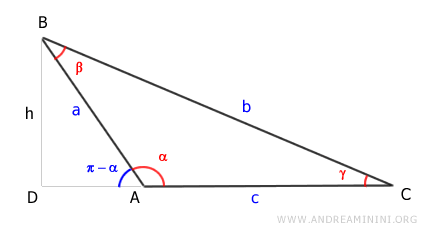
Substituting h with \(a \cdot \sin(\pi - \alpha)\):

$$ Area = \frac{1}{2} \cdot c \cdot h $$

$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin(\pi - \alpha) $$

The angle (π - α) is the supplementary angle of the obtuse angle α.

Using the property of associated angles, where \(\sin(\pi - \alpha) = \sin(\alpha)\), the formula simplifies to:

$$ Area = \frac{1}{2} \cdot c \cdot a \cdot \sin(\alpha) $$

Here, α is the obtuse angle between sides a and c of the scalene triangle.

Thus, the formula is once again validated.

In conclusion, this formula for calculating the area applies universally to any type of triangle.