Linear Trigonometric Equations in Sine and Cosine
A trigonometric equation is called a linear equation in sine and cosine when it can be expressed in the form $$ a \sin x + b \cos x + c = 0 $$ where \( a \), \( b \), and \( c \) are real coefficients, with \( a \neq 0 \) and \( b \neq 0 \).
How to Solve Linear Trigonometric Equations
These equations can be solved efficiently by reducing them to simpler forms using algebraic methods.
- If the constant term is zero (\( c = 0 \)), divide through by cosine. This transforms the equation into an elementary trigonometric equation involving the tangent function: $$ a \sin x + b \cos x = 0 $$ $$ a \frac{\sin x}{\cos x} + b \frac{\cos x}{\cos x} = \frac{0}{\cos x} $$ $$ a \tan x + b = 0 $$ $$ \tan x = -\frac{b}{a} $$
- If the constant term is not zero (\( c \neq 0 \)), use parametric formulas: $$ a \sin x + b \cos x + c = 0 $$ $$ a \frac{2t}{1+t^2} + b \frac{1-t^2}{1+t^2} + c = 0 $$ Here, the variable \( t \) is defined as: $$ t = \tan \frac{x}{2} $$ Note that the tangent is undefined for \( \pi \) radians (180°). Therefore, the equation must not include solutions where: $$ x = \pi + 2k \pi $$
Note: Alternatively, you can substitute sine and cosine using the fundamental trigonometric identity: $$ \sin^2 x + \cos^2 x = 1 $$ which gives: $$ \sin x = \pm \sqrt{1 - \cos^2 x} $$ $$ \cos x = \pm \sqrt{1 - \sin^2 x} $$
Example
Let’s solve the following trigonometric equation:
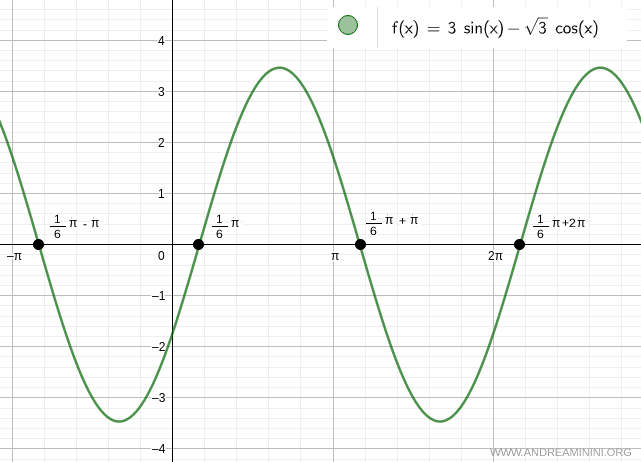
$$ 3 \sin x - \sqrt{3} \cos x = 0 $$
This is a linear equation in sine and cosine with no constant term (\( c = 0 \)).
Divide through by \( \cos x \) to rewrite the equation as an elementary equation in tangent:
$$ 3 \frac{\sin x}{\cos x} - \sqrt{3} \frac{\cos x}{\cos x} = \frac{0}{\cos x} $$
$$ 3 \tan x - \sqrt{3} = 0 $$
Rearrange to isolate the tangent:
$$ \tan x = \frac{\sqrt{3}}{3} $$
Finally, solve for \( x \) by taking the arctangent of both sides:
$$ \arctan(\tan x) = \arctan\left(\frac{\sqrt{3}}{3}\right) $$
$$ x = \arctan\left(\frac{\sqrt{3}}{3}\right) $$
The arctangent of \( \sqrt{3}/3 \) is \( \pi/6 \):
$$ x = \frac{\pi}{6} $$
Since the tangent function is periodic with a period of \( \pi \) (180°), there are infinitely many solutions spaced \( \pi \) radians apart:
$$ x = \frac{\pi}{6} + k \pi $$
where \( k \) is any integer.
Example 2
Next, solve this equation:
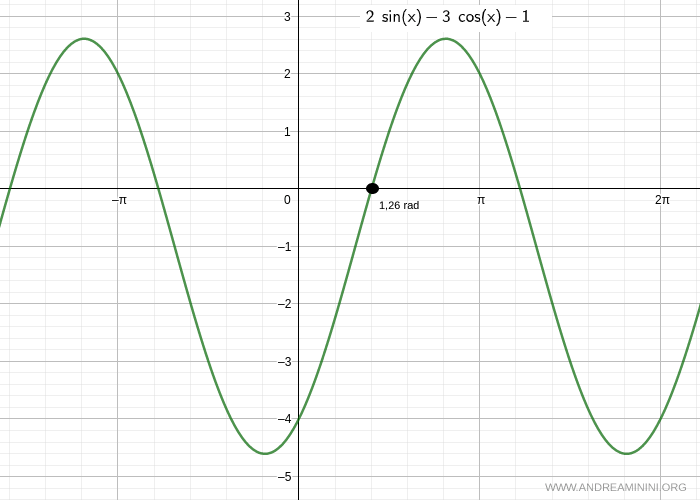
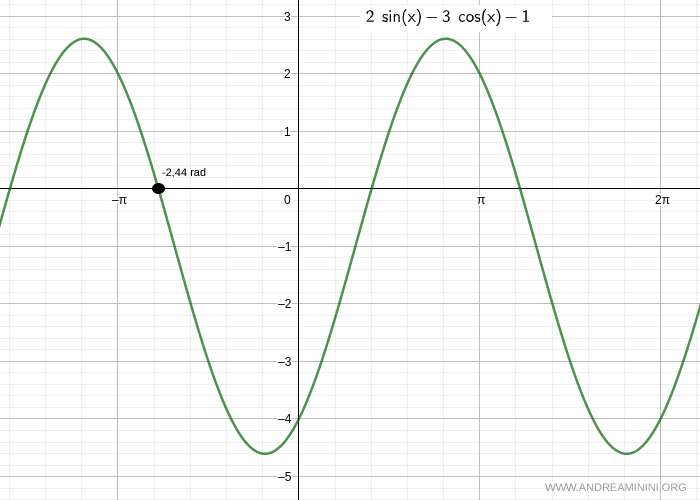
$$ 2 \sin x - 3 \cos x - 1 = 0 $$
This is a linear equation in sine and cosine.
First, check if \( x = \pi/2 \) is a solution:
$$ 2 \sin\left(\frac{\pi}{2}\right) - 3 \cos\left(\frac{\pi}{2}\right) - 1 = 0 $$
$$ 2 \cdot 1 - 3 \cdot 0 - 1 = 0 $$
$$ 2 - 1 = 0 $$
$$ 1 = 0 $$
Since \( \pi/2 \) is not a solution, proceed as follows:
Substitute sine and cosine with their parametric formulas, where \( t = \tan(x/2) \):
$$ a \frac{2t}{1+t^2} + b \frac{1-t^2}{1+t^2} + c = 0 $$
Here, \( a = 2, b = -3, c = -1 \):
$$ 2 \frac{2t}{1+t^2} - 3 \frac{1-t^2}{1+t^2} - 1 = 0 $$
Simplify the equation:
$$ \frac{4t - 3 + 3t^2 - (1 + t^2)}{1 + t^2} = 0 $$
$$ \frac{2t^2 + 4t - 4}{1 + t^2} = 0 $$
Eliminate the denominator by multiplying through by \( 1 + t^2 \):
$$ 2t^2 + 4t - 4 = 0 $$
Divide through by 2:
$$ t^2 + 2t - 2 = 0 $$
Solve this quadratic equation:
$$ t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
$$ t = \frac{-2 \pm \sqrt{4 + 8}}{2} $$
$$ t = \frac{-2 \pm \sqrt{12}}{2} = \begin{cases} t_1 = \frac{-2 + \sqrt{12}}{2} \\ \\ t_2 = \frac{-2 - \sqrt{12}}{2} \end{cases} $$
Since \( t = \tan(x/2) \), the first solution is:
$$ \tan \frac{x}{2} = \frac{-2 + \sqrt{12}}{2} $$
Take the arctangent of both sides:
$$ \frac{x}{2} = \arctan\left(\frac{-2 + \sqrt{12}}{2}\right) + k \pi $$
Here, the arctangent evaluates to approximately 0.63 radians (36.21°):
$$ \frac{x}{2} = 0.63 \, \text{rad} + k \pi $$
$$ x = 1.26 \, \text{rad} + 2k \pi $$
The second solution is:
$$ \tan \frac{x}{2} = \frac{-2 - \sqrt{12}}{2} $$
Taking the arctangent:
$$ \frac{x}{2} = \arctan\left(\frac{-2 - \sqrt{12}}{2}\right) + k \pi $$
The arctangent evaluates to approximately -1.22 radians (-69.9°):
$$ \frac{x}{2} = -1 .22 \, \text{rad} + k \pi $$
$$ x = -2.44 \, \text{rad} + 2k \pi $$
And so forth.
