Solving the Equation sin x = sin y

The trigonometric equation sin α = sin α' is satisfied when the angles are either congruent, α = α', or supplementary, meaning α + α' = π. $$ α = α' + 2k \pi $$ or $$ α + α' = \pi + 2k \pi $$

Since sine is a periodic function with a period of 2π, this trigonometric equation has infinitely many solutions, taking into account integer multiples of a full rotation (2π).

Here, k represents any integer, positive or negative.

An Example Solution

Let's solve the following equation:

$$ \sin \left( \frac{1}{2}x + \frac{\pi}{2} \right) = \sin \left( \frac{1}{6}x + \frac{\pi}{6} \right) $$

The angles in the two sine functions are:

$$ \alpha = \frac{1}{2}x + \frac{\pi}{2} $$

$$ \alpha' = \frac{1}{6}x + \frac{\pi}{6} $$

Using the formula for the equation sin x = sin y:

$$ α = α' + 2k \pi \ or \ α + α' = \pi + 2k \pi $$

Substituting α and α':

$$ \frac{1}{2}x + \frac{\pi}{2} = \frac{1}{6}x + \frac{\pi}{6} + 2k \pi \ or \ \frac{1}{2}x + \frac{\pi}{2} + \frac{1}{6}x + \frac{\pi}{6} = \pi + 2k \pi $$

We solve for x:

$$ \frac{1}{2}x - \frac{1}{6}x = \frac{\pi}{6} - \frac{\pi}{2} + 2k \pi \ or \ \frac{3+1}{6}x + \frac{3\pi + \pi}{6} = \pi + 2k \pi $$

$$ \frac{3 - 1}{6}x = \frac{\pi - 3\pi}{6} + 2k \pi \ or \ \frac{4}{6}x + \frac{4\pi}{6} = \pi + 2k \pi $$

$$ \frac{2}{6}x = \frac{-2\pi}{6} + 2k \pi \ or \ \frac{2}{3}x + \frac{2\pi}{3} = \pi + 2k \pi $$

$$ \frac{1}{3}x = \frac{-\pi}{3} + 2k \pi \ or \ \frac{2}{3}x = \pi - \frac{2\pi}{3} + 2k \pi $$

$$ x = 3 \left( \frac{-\pi}{3} + 2k \pi \right) \ or \ \frac{2}{3}x = \frac{3\pi - 2\pi}{3} + 2k \pi $$

$$ x = -\pi + 6k \pi \ or \ \frac{2}{3} x = \frac{\pi}{3} + 2k \pi $$

$$ x = -\pi + 6k \pi \ or \ x = \frac{3}{2} \left( \frac{\pi}{3} + 2k \pi \right) $$

$$ x = -\pi + 6k \pi \ or \ x = \frac{3}{2} \cdot \frac{\pi}{3} + \frac{3}{2} \cdot 2k \pi $$

$$ x = -\pi + 6k \pi \ or \ x = \frac{\pi}{2} + 3k \pi $$

These are all the solutions for the equation sin x = sin y

$$ x = -\pi + 6k \pi \ or \ x = \frac{\pi}{2} + 3k \pi $$

Now we can verify if these solutions satisfy the trigonometric equation.

Verification for k=0

$$ x = -\pi + 6(0) \pi \ or \ x = \frac{\pi}{2} + 3(0) \pi $$

$$ x = -\pi \ or \ x = \frac{\pi}{2} $$

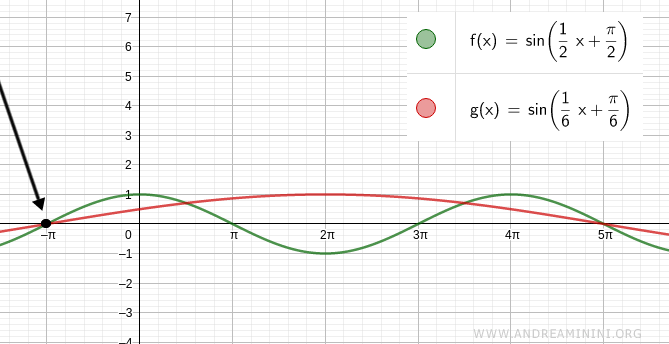
Substitute the first solution x = -π into the equation:

$$ \sin \left( \frac{1}{2}x + \frac{\pi}{2} \right) = \sin \left( \frac{1}{6}x + \frac{\pi}{6} \right) $$

$$ \sin \left( \frac{1}{2} (-\pi) + \frac{\pi}{2} \right) = \sin \left( \frac{1}{6} (-\pi) + \frac{\pi}{6} \right) $$

$$ \sin (0) = \sin (0) $$

$$ 0 = 0 $$

Which is indeed satisfied.

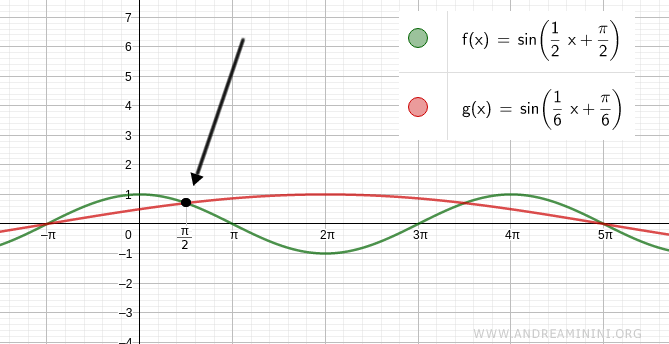
Substitute the second solution x = π/2 into the equation:

$$ \sin \left( \frac{1}{2}x + \frac{\pi}{2} \right) = \sin \left( \frac{1}{6}x + \frac{\pi}{6} \right) $$

$$ \sin \left( \frac{1}{2} \cdot \frac{\pi}{2} + \frac{\pi}{2} \right) = \sin \left( \frac{1}{6} \cdot \frac{\pi}{2} + \frac{\pi}{6} \right) $$

$$ \sin \left( \frac{3\pi}{4} \right) = \sin \left( \frac{\pi}{4} \right) $$

$$ 0.71 = 0.71 $$

Which is also satisfied.

Verification for k=1

$$ x = -\pi + 6(1) \pi \ or \ x = \frac{\pi}{2} + 3(1) \pi $$

$$ x = 5\pi \ or \ x = \frac{\pi}{2} + 3\pi $$

$$ x = 5\pi \ or \ x = \frac{7\pi}{2} $$

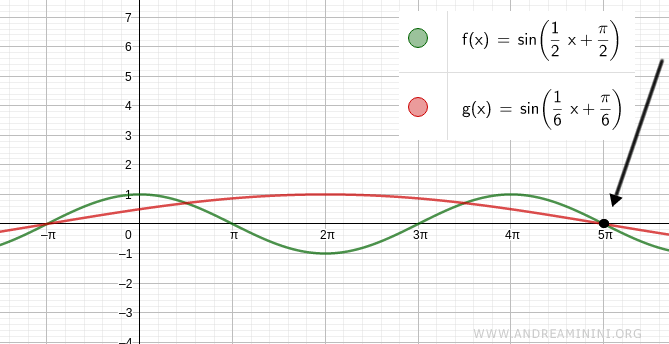
Substitute the first solution x = 5π into the equation:

$$ \sin \left( \frac{1}{2}x + \frac{\pi}{2} \right) = \sin \left( \frac{1}{6}x + \frac{\pi}{6} \right) $$

$$ \sin (3\pi) = \sin (\pi) $$

This holds true as sin(3π) = 0 and sin(π) = 0.

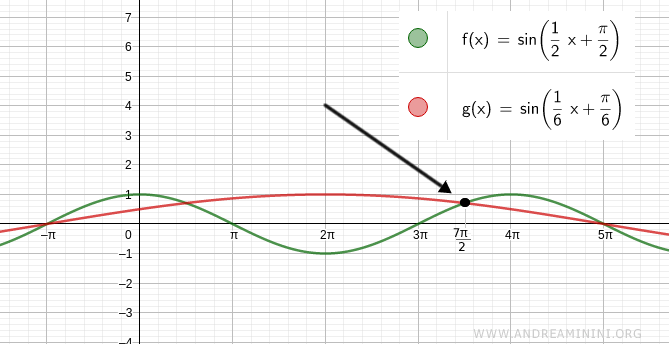
Substitute the second solution x = 7π/2 into the equation:

$$ \sin ( \frac{1}{2}x + \frac{\pi}{2} ) = \sin ( \frac{1}{6}x + \frac{\pi}{6} ) $$

$$ \sin ( \frac{1}{2} \cdot \frac{7 \pi}{2} + \frac{\pi}{2} ) = \sin ( \frac{1}{6} \cdot \frac{7 \pi}{2} + \frac{\pi}{6} ) $$

$$ \sin ( \frac{7 \pi}{4} + \frac{\pi}{2} ) = \sin ( \frac{7 \pi}{12} + \frac{\pi}{6} ) $$

$$ \sin ( \frac{7 \pi + 2 \pi}{4} ) = \sin ( \frac{7 \pi + 2 \pi }{12} ) $$

$$ \sin ( \frac{9 \pi}{4} ) = \sin ( \frac{9 \pi }{12} ) $$

$$ \sin ( \frac{9 \pi}{4} ) = \sin ( \frac{3 \pi }{4} ) $$

$$ 0,71 = 0,71 $$

Which is also confirmed.

The Proof

Let's consider two angles, α₁ and α₂, that yield the same sine value:

$$ \sin \alpha_1 = \sin \alpha_2 = c $$

Two angles share the same sine value in exactly two cases:

1. if the angles are congruent (α₁ = α₂)
2. if the angles are supplementary (α₁ + α₂ = π)

Graphically:

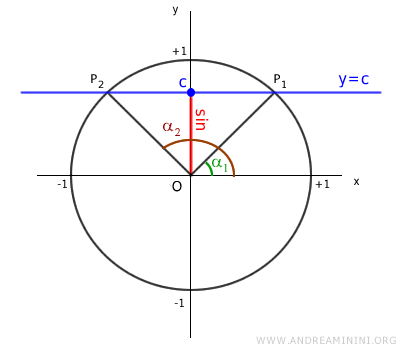
Thus, the conditions for achieving the same sine value are:

$$ \alpha_1 = \alpha_2 $$ $$ \alpha_1 + \alpha_2 = \pi $$

Sine is a periodic function with a period of 2π.

So, we also consider multiples k of a full rotation, 2π, as possible solutions:

$$ \alpha_1 = \alpha_2 + 2k \pi $$ $$ \alpha_1 + \alpha_2 = \pi + 2k \pi $$

This completes the solution set for equations where sin α₁ = sin α₂.

$$ \alpha_1 = \alpha_2 + 2k \pi \ or \ \alpha_1 + \alpha_2 = \pi + 2k \pi $$

And so on.