Trigonometric Equation cos x = c
The trigonometric equation $$ \cos x = c $$ is a straightforward trigonometric equation where the unknown variable x is the argument of the cosine function, while c represents any real number.
This equation, cos x = c, only has solutions if c falls within the interval c ∈ [-1,1].
$$ -1 \le c \le 1 $$
If c is outside the closed interval [-1,1], then the equation has no solutions since c does not lie within the range of the cosine function.
Note: In trigonometry, the cosine function’s values range between -1 and 1.
If the equation cos x = c has a solution, it will have infinitely many solutions of the form α+2πk or -α+2πk.
$$ x = \alpha + 2\pi k \vee -\alpha + 2\pi k $$
To solve the equation, we find the angle α by applying the inverse cosine function, or arccosine.
$$ \arccos c = \alpha $$
The arccosine function gives us the angle α for which cos α = c.
An Example
Let's check if this trigonometric equation has any solutions:
$$ \cos x = \frac{1}{2} $$
This equation is valid because the constant term lies within the cosine’s range of possible values.
$$ -1 \le \frac{1}{2} \le 1 $$
Thus, this trigonometric equation has the following solutions:
$$ x = \alpha + 2\pi k \vee -\alpha + 2\pi k $$
To find the angle α, we calculate the arccosine of 1/2, which is π/3 (or 60°).
$$ \arccos \frac{1}{2} = \frac{\pi}{3} $$
Substituting α = π/3 into the solution formula gives:
$$ x = \alpha + 2\pi k \vee -\alpha + 2\pi k $$
$$ x = \frac{\pi}{3} + 2\pi k \vee - \frac{\pi}{3} + 2\pi k $$
Graphically, the solutions are shown as follows:
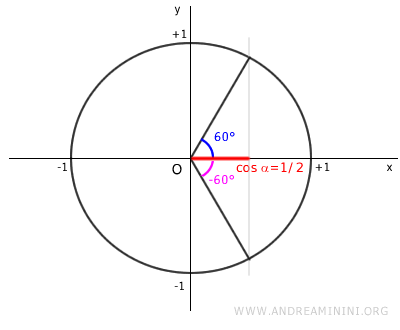
Both π/3 rad (60°) and -π/3 rad (-60°) satisfy cos x = 1/2.
Since cosine is a periodic function, I also include integer multiples of 2πk in the solution set.
$$ x = \frac{\pi}{3} + 2\pi k \vee -\frac{\pi}{3} + 2\pi k $$
Therefore, the equation cos x = 1/2 has infinitely many solutions of the form π/3 + 2πk and -π/3 + 2πk.
Explanation
We begin by plotting the unit circle on the Cartesian plane.
The unit circle has a radius of 1.
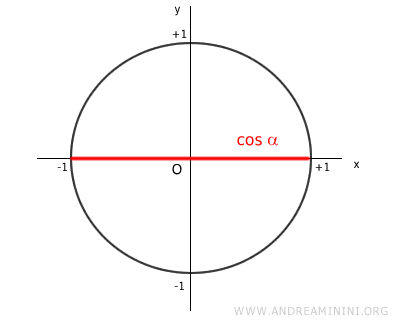
The value of the cosine function is measured along the x-axis, ranging from -1 to +1 (the range of cosine).
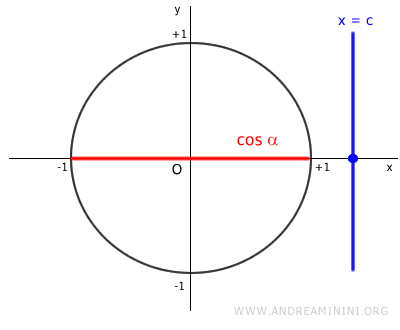
Let’s consider any real value c to determine if the trigonometric equation has solutions.
If c is greater than 1, the line x = c runs parallel to the y-axis, meaning it does not intersect the unit circle.
As a result, no angle x within the cosine function can yield a value of c greater than one.
Similarly, if c is less than -1, no angle x in the cosine function will result in c.
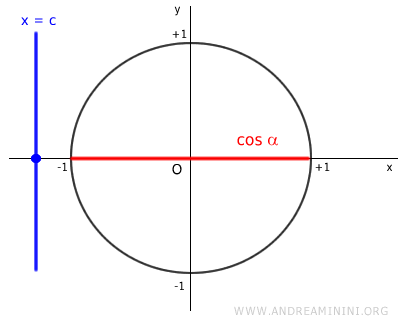
Thus, the equation cos x = c can only have solutions if c is within the interval [-1,1].
$$ -1 \le c \le 1 $$
Now, let’s look at a case where c is within [-1,1].
The line x = c runs parallel to the y-axis, intersecting the unit circle at two points, P1 and P2.
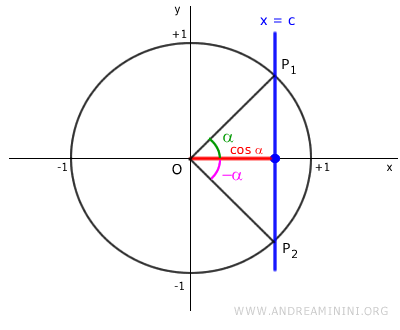
Points P1 and P2 mark the endpoints of the angles α and -α. Since cosine is an even function, -α is simply the opposite angle of α.
So, for this value of c, there are two angles α and -α that satisfy cos x = c:
$$ \cos \alpha = \cos (-\alpha) = c $$
Both solutions α and -α satisfy the equation, so we can write:
$$ x = \alpha \vee -\alpha $$
However, these aren’t the only possible solutions.
Since cosine is a periodic function that repeats its values every period of 2π, we also add integer multiples of 2πk to α and -α:
$$ x = \alpha + 2\pi k \vee -\alpha + 2\pi k $$
Therefore, if c is within the interval [-1,1], the equation cos x = c has infinitely many solutions: x = α+2πk or -α+2πk.
$$ \cos x = c $$
Note: In the special cases where c = 1 or c = -1, the line x = c intersects the unit circle at only one point instead of two, which also counts as a solution: $$ \alpha = - \alpha = 0 $$
To find the angle α, we apply the arccosine function to both sides:
$$ \arccos( \cos x ) = \arccos c $$
The arccosine function is the inverse of cosine.
This means that arccos(cos x) = x:
$$ x = \arccos c $$
With the angle α, we also find the opposite angle -α.
And so forth.
