Trigonometric Equation cos(a) = cos(b)

The trigonometric equation $$ \cos(\alpha) = \cos(\alpha') $$ holds true when the angles are either congruent, α=α', or opposites, α=-α'. Specifically, this results in $$ \alpha=\alpha'+2k \pi \ $$ or $$  \alpha = -\alpha' + 2k \pi $$

Because cosine is a periodic function with a period of 2π, this trigonometric equation has infinitely many solutions when we account for integer multiples k of a full rotation 2π.

Here, k is any integer within the range (-∞, ∞).

A Practical Example

Let’s solve the trigonometric equation:

$$ \cos\left(\frac{1}{2}x\right) = \cos\left(\frac{3}{2}x\right) $$

The angles in each cosine function are:

$$ \alpha_1 = \frac{1}{2}x $$

$$ \alpha_2 = \frac{3}{2}x $$

We use the trigonometric identity for cos x = cos y:

$$ \alpha = \alpha' + 2k \pi \ \text{or} \ \alpha = - \alpha' + 2k \pi $$

Substitute α and α':

$$ \frac{1}{2}x = \frac{3}{2}x + 2k \pi \ \text{or} \ \frac{1}{2}x = - \frac{3}{2}x + 2k \pi $$

We simplify to isolate x:

$$ \frac{1}{2}x - \frac{3}{2}x = 2k \pi \ \text{or} \ \frac{1}{2}x + \frac{3}{2}x = 2k \pi $$

$$ - x = 2k \pi \ \text{or} \ 2x = 2k \pi $$

$$ x = -2k \pi \ \text{or} \ x = k \pi $$

This gives all solutions for cos x = cos y by varying the integer k.

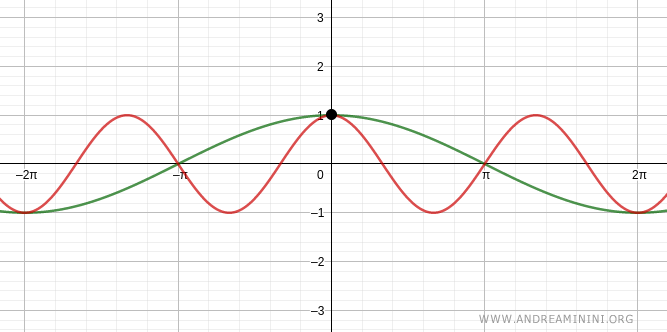
Verification for k = 0

$$ x = -2(0) \pi \ \text{or} \ x = (0) \pi $$

$$ x = 0 \ \text{or} \ x = 0 $$

A solution to the trigonometric equation is x=0.

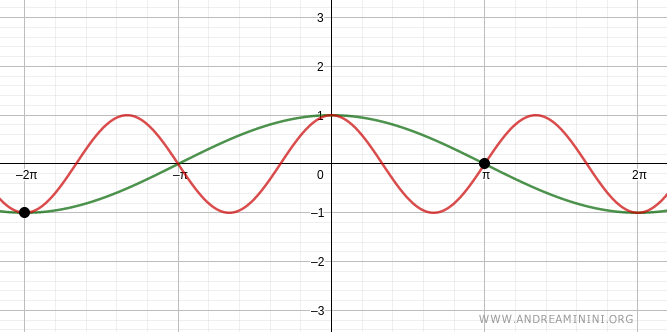
Verification for k = 1

$$ x = -2(1) \pi \ \text{or} \ x = (1) \pi $$

$$ x = -2 \pi \ \text{or} \ x = \pi $$

Two additional solutions are x = -2π and x = π.

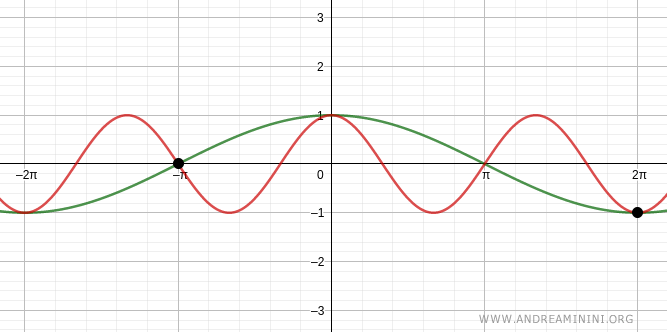
Verification for k = -1

$$ x = -2(-1) \pi \ \text{or} \ x = (-1) \pi $$

$$ x = 2 \pi \ \text{or} \ x = -\pi $$

Another pair of solutions is x = 2π and x = -π.

By varying k, we can obtain the infinite solutions to this trigonometric equation.

The Proof

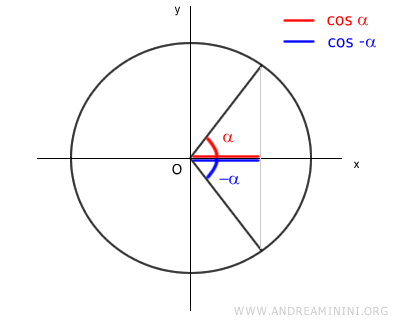
Consider two angles, α₁ and α₂, that produce the same cosine value:

$$ \cos \alpha_1 = \cos \alpha_2 = c $$

Two angles have the same cosine value in two cases:

• when the angles are congruent (α₁=α₂)
• when the angles are opposites (α₁=-α₂)

Graphically, this appears as:

Thus, the conditions for equal cosine values are:

$$ \alpha_1 = \alpha_2 $$

$$ \alpha_1 = - \alpha_2 $$

Since cosine is a periodic function with a period of 2π, we also need to include integer multiples k of a full rotation, 2π, among the solutions.

$$ \alpha_1 = \alpha_2 + 2k \pi $$

$$ \alpha_1 = - \alpha_2 + 2k \pi $$

This completes the solution set for a trigonometric equation of the form cos α₁ = cos α₂:

$$ \alpha_1 = \alpha_2 + 2k \pi \ \text{or} \ \alpha_1 = - \alpha_2 + 2k \pi $$

And so on.