Trigonometric Inequalities

What are trigonometric inequalities?

Trigonometric inequalities are inequalities where the variable x appears as the argument of one or more trigonometric functions, such as sine, cosine, tangent, or cotangent.

Trigonometric inequalities can be categorized as:

• Elementary trigonometric inequalities
  These involve a single trigonometric function (e.g., sine, cosine, tangent, etc.) with the variable x as its argument, compared to a constant value c. For example, $$ \sin x \le c $$
• Non-elementary trigonometric inequalities
  These involve two or more trigonometric functions with the variable x as their argument, compared to a constant value c. For example, $$ \sin x + \cos x \le c $$

How to Solve Trigonometric Inequalities

To solve a trigonometric inequality:

1. Find the solutions of the associated trigonometric equation.
2. Identify the angles that satisfy the inequality.

From a graphical perspective, plot the graph of the trigonometric function (e.g., sin x = c).

Then, draw the horizontal line y = c and determine the x-values where the inequality holds true.

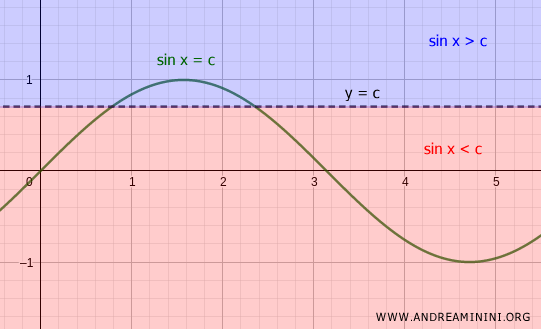
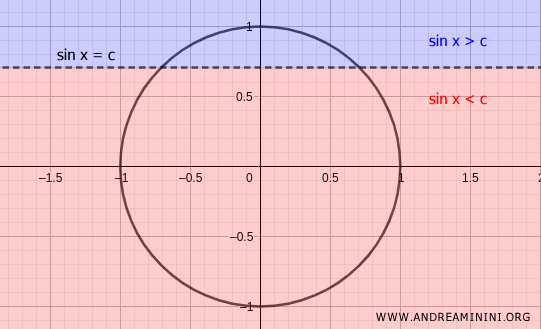
Alternatively, use the unit circle by drawing the line sin x = c.

Identify the points of intersection between the line and the circle, and determine the angles that satisfy the inequality.

An Example

Let’s solve the following elementary trigonometric inequality:

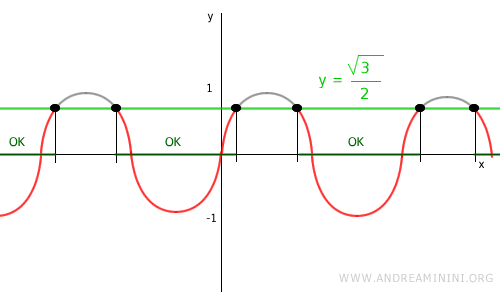
$$ \sin x \le \frac{\sqrt{3}}{2} $$

First, solve the associated trigonometric equation:

$$ \sin x = \frac{\sqrt{3}}{2} $$

The solutions of the elementary sine equation are:

$$ x = \frac{\pi}{3} + 2k \pi \ \text{or} \ \pi - \frac{\pi}{3} + 2k \pi $$

To find these solutions graphically, draw the horizontal line y=√3/2 and locate its points of intersection with the unit circle (A and B).

Then, add 2kπ to account for the periodic nature of the sine function.

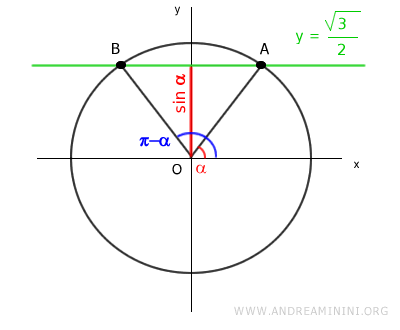
It becomes evident that, within the interval [0, 2π], the inequality is satisfied in the ranges:

$$ x \in (0, \frac{\pi}{3}) \cup (\pi - \frac{\pi}{3}, 2 \pi) $$

Note: Alternatively, you can analyze the graph of the trigonometric function by plotting y=√3/2 and identifying the x-values where the line intersects the curve.

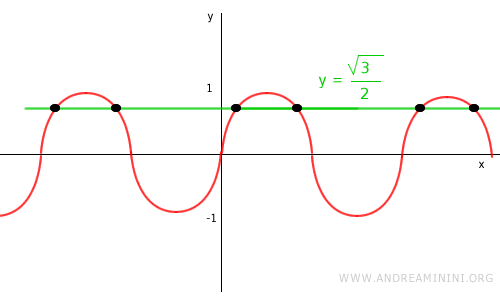
Then, determine the intervals of x where the inequality holds true.

Example 2

Now, consider this trigonometric inequality:

$$ 2 \sin^2 x + \sqrt{3} \sin x \ge 0 $$

This is a non-elementary trigonometric inequality.

$$ 2 \sin^2 x + \sqrt{3} \sin x = 0 $$

Using the substitution t = sin x:

$$ 2t^2 + \sqrt{3}t = 0 $$

Solve the quadratic equation with coefficients a=2, b=√3, c=0:

$$ t = \frac{-b \pm \sqrt{b^2-4ac}}{2a} $$

$$ t = \frac{-(\sqrt{3}) \pm \sqrt{(\sqrt{3})^2-4(2)(0)}}{4} $$

$$ t = \frac{-\sqrt{3} \pm \sqrt{3}}{4} $$

$$ t = \begin{cases} t_1 = 0 \\ t_2 = -\frac{\sqrt{3}}{2} \end{cases} $$

The solutions are t₁=0 and t₂=-√3/2.

The inequality represents a parabola opening upward because a > 0.

Thus, the inequality $$ t^2 + \sqrt{3}t \ge 0 $$ is satisfied in the intervals:

$$ t \in (-\infty, -\frac{\sqrt{3}}{2}] \cup [0, +\infty) $$

Since t = sin x:

$$ \sin x \in (-1, -\frac{\sqrt{3}}{2}] \cup [0, 1) $$

Using the unit circle, determine the angles that satisfy the inequality:

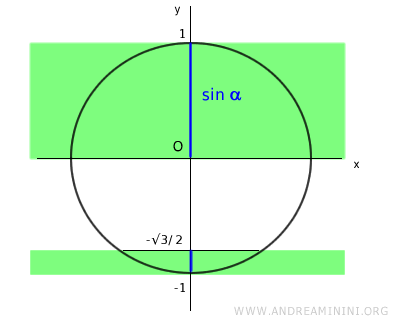
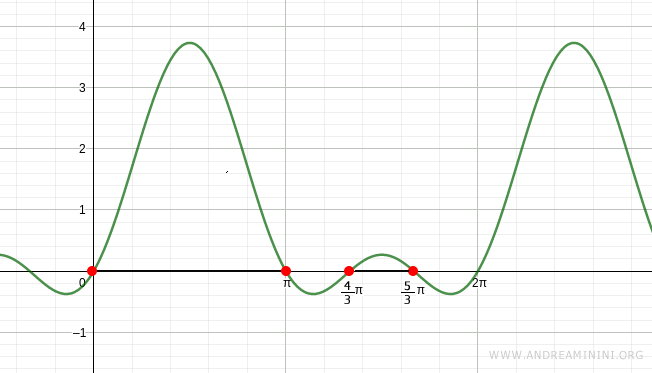
• sin x is between -1 and -√3/2 in the interval $$ x \in [\frac{4}{3} \pi, \frac{5}{3} \pi] $$
• sin x is between 0 and 1 in the interval $$ x \in [0, \pi] $$

Therefore, within a full rotation (0, 2π), the inequality holds for:

$$ \frac{4}{3} \pi \le x \le \frac{5}{3} \pi \ \text{or} \ 0 \le x \le \pi $$

Considering the periodic nature of the sine function, add 2kπ to the solutions:

$$ \frac{4}{3} \pi + 2k \pi \le x \le \frac{5}{3} \pi + 2k \pi \ \text{or} \ 0 + 2k \pi \le x \le \pi + 2k \pi $$

where k is any integer.

The graph of the trigonometric function confirms these results:

And so on.