Trigonometric Equation: cos(a) = -cos(b)

The trigonometric equation $$ \cos \alpha = -\cos \alpha' $$ can be solved using the formula $$ \cos \alpha = \cos (\pi - \alpha') $$ which leads to the solutions $$ \alpha = (\pi - \alpha') + 2k \pi \ ∨ \ \alpha = - (\pi - \alpha') + 2k \pi $$

Example

Let’s solve the trigonometric equation:

$$ \cos\left(\frac{1}{2}x\right) = - \cos\left(\frac{3}{4}x\right) $$

We rewrite it in an equivalent form:

$$ \cos\left(\frac{1}{2}x\right) = \cos\left(\pi - \frac{3}{4}x\right) $$

This allows us to treat it as an equation of the form cos(α) = cos(α'), where:

$$ \alpha = \frac{1}{2}x $$

$$ \alpha' = \pi - \frac{3}{4}x $$

Using the standard formula for cos(α) = cos(α'), the solutions are:

$$ \alpha = \alpha' + 2k \pi \ ∨ \ \alpha = - \alpha' + 2k \pi $$

Substituting the values of α and α':

$$ \frac{1}{2}x = \left(\pi - \frac{3}{4}x\right) + 2k \pi \ ∨ \ \frac{1}{2}x = -\left(\pi - \frac{3}{4}x\right) + 2k \pi $$

Simplifying the equations:

$$ \frac{1}{2}x + \frac{3}{4}x = \pi + 2k \pi \ ∨ \ \frac{1}{2}x - \frac{3}{4}x = -\pi + 2k \pi $$

$$ \frac{5}{4}x = \pi + 2k \pi \ ∨ \ -\frac{1}{4}x = -\pi + 2k \pi $$

$$ x = \frac{4}{5}(\pi + 2k \pi) \ ∨ \ -x = 4(-\pi + 2k \pi) $$

$$ x = \frac{4}{5}\pi + \frac{4}{5}\cdot 2k \pi \ ∨ \ -x = -4\pi + 8k \pi $$

$$ x = \frac{4}{5}\pi + \frac{4}{5}\cdot 2k \pi \ ∨ \ x = 4\pi - 8k \pi $$

We now have the general solution, where k is any integer (positive, zero, or negative), giving us an infinite number of solutions.

To find specific solutions, we assign values to k.

Verification for k = 0

$$ x = \frac{4}{5}\pi + \frac{4}{5}\cdot 2k \pi \ ∨ \ x = 4\pi - 8k \pi $$

$$ x = \frac{4}{5}\pi + \frac{4}{5}\cdot 2(0)\pi \ ∨ \ x = 4\pi - 8(0)\pi $$

$$ x = \frac{4}{5}\pi \ ∨ \ x = 4\pi $$

Thus, the first two solutions are x = 4π/5 and x = 4π.

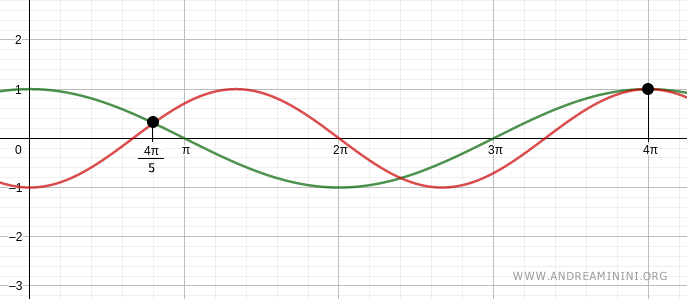
Verification for k = 1

$$ x = \frac{4}{5}\pi + \frac{4}{5}\cdot 2k \pi \ ∨ \ x = 4\pi - 8k \pi $$

$$ x = \frac{4}{5}\pi + \frac{4}{5}\cdot 2(1)\pi \ ∨ \ x = 4\pi - 8(1)\pi $$

$$ x = \frac{4}{5}\pi + \frac{8}{5}\pi \ ∨ \ x = 4\pi - 8\pi $$

$$ x = \frac{12}{5}\pi \ ∨ \ x = -4\pi $$

Two additional solutions are x = 12π/5 and x = -4π.

 

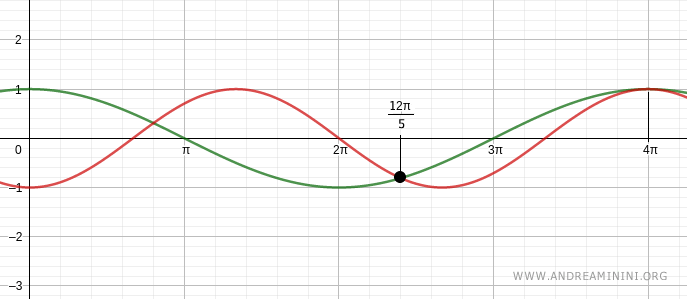
By varying k, we can determine all other infinite solutions.

Proof

Two angles α and α' have opposite cosine values:

$$ \cos \alpha = - \cos \alpha' $$

if and only if they are supplementary angles.

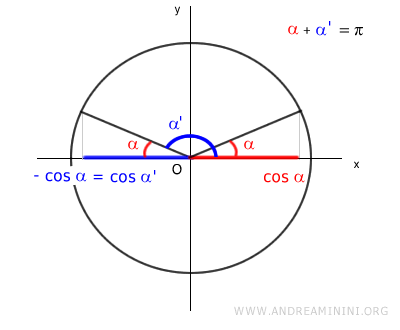
The sum of two supplementary angles is 180° (or π radians):

$$ \alpha + \alpha' = \pi $$

$$ \alpha = \pi - \alpha' $$

Substituting α with π - α':

$$ \cos \alpha = - \cos \alpha' $$

$$ \cos (\pi - \alpha') = - \cos \alpha' $$

Combining these equations, we get the equivalence:

$$ \cos \alpha = - \cos \alpha' = \cos (\pi - \alpha') $$

which simplifies to:

$$ \cos \alpha = \cos (\pi - \alpha') $$

This reduces the equation to the standard form of cos(x) = cos(y):

$$ x = y + 2k \pi \ ∨ \ x = -y + 2k \pi $$

where x = α and y = π - α':

$$ \alpha = (\pi - \alpha') + 2k \pi \ ∨ \ \alpha = -(\pi - \alpha') + 2k \pi $$

And so on.