Trigonometric Equations of the Form sin(α) = cos(α')

The trigonometric equation $$ \sin \alpha = \cos \alpha' $$ can be solved using the formula $$ \sin \alpha = \sin (\frac{\pi}{2} - \alpha') $$. The solutions are given by $$ \alpha = (\frac{\pi}{2} - \alpha') + 2k \pi \ \text{or} \ \alpha + (\frac{\pi}{2} - \alpha') = \pi + 2k \pi $$

Example

Let’s solve the trigonometric equation:

$$ \sin(\frac{1}{2}x) = \cos(\frac{1}{4}x) $$

We rewrite the cosine function, cos(1/4x), as a sine function: sin(π/2 - 1/4x).

$$ \sin(\frac{1}{2}x) = \sin(\frac{\pi}{2} - \frac{1}{4}x) $$

This transforms the equation into one of the form sin α = sin α', where:

$$ \alpha = \frac{1}{2}x $$

$$ \alpha' = \frac{\pi}{2} - \frac{1}{4}x $$

We then apply the formula for solving an equation of the form sin α = sin α':

$$ \alpha = \alpha' + 2k \pi \ \text{or} \ \alpha + \alpha' = \pi + 2k \pi $$

Here, k is any integer.

Substituting the values of α and α':

$$ \frac{1}{2}x = (\frac{\pi}{2} - \frac{1}{4}x) + 2k \pi \ \text{or} \ \frac{1}{2}x + (\frac{\pi}{2} - \frac{1}{4}x) = \pi + 2k \pi $$

Now, we simplify and isolate x:

$$ \frac{1}{2}x + \frac{1}{4}x = \frac{\pi}{2} + 2k \pi \ \text{or} \ \frac{1}{2}x - \frac{1}{4}x = \pi + 2k \pi - \frac{\pi}{2} $$

$$ \frac{3}{4}x = \frac{\pi}{2} + 2k \pi \ \text{or} \ \frac{1}{4}x = \frac{\pi}{2} + 2k \pi $$

$$ x = \frac{4}{3} \cdot (\frac{\pi}{2} + 2k \pi) \ \text{or} \ x = 4 \cdot (\frac{\pi}{2} + 2k \pi) $$

$$ x = \frac{2 \pi}{3} + \frac{8k \pi}{3} \ \text{or} \ x = 2 \pi + 8k \pi $$

In this way, we obtain all the solutions to the equation sin x = sin y.

Next, we verify whether these solutions satisfy the original trigonometric equation.

Verification for k = 0

$$ x = \frac{2 \pi}{3} + \frac{8k \pi}{3} \ \text{or} \ x = 2 \pi + 8k \pi $$

$$ x = \frac{2 \pi}{3} + \frac{8(0) \pi}{3} \ \text{or} \ x = 2 \pi + 8(0) \pi $$

$$ x = \frac{2 \pi}{3} \ \text{or} \ x = 2 \pi $$

Thus, one solution to the equation is x = 2π/3, and another is x = 2π.

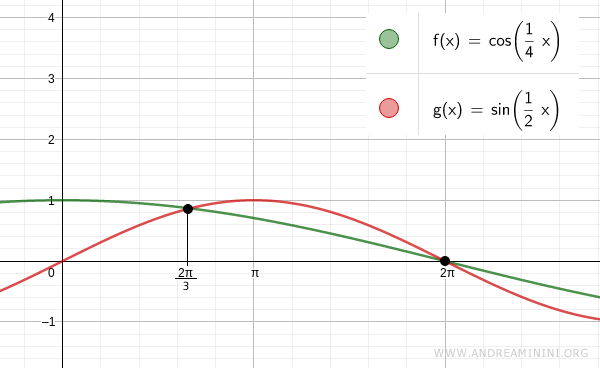
By varying k (e.g., k = 1, k = -1, k = 2, etc.), we can find all the other infinite solutions of the equation.

 

Proof

The cosine function:

$$ \cos \alpha $$

can be rewritten in terms of the sine function using an associated angle:

$$ \cos \alpha = \sin (\frac{\pi}{2} - \alpha) $$

Sine and cosine are offset by 90° (π/2).

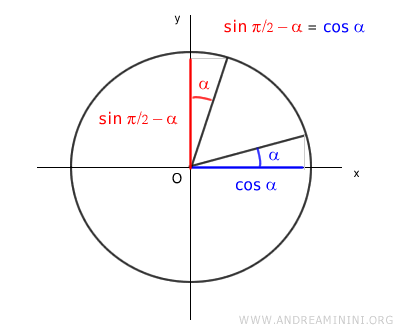
By subtracting the angle α from 90° (π/2), we can express the cosine function cos(α) as the sine function sin(π/2 - α).

Thus, the trigonometric equation:

$$ \sin \alpha = \cos \alpha' $$

can be rewritten as:

$$ \sin \alpha = \sin (\frac{\pi}{2} - \alpha') $$

This transforms the equation into an identity between two sine functions sin(α) = sin(β), with solutions:

$$ \alpha = \beta + 2k \pi \ \text{or} \ \alpha + \beta = \pi + 2k \pi $$

Here, β = π/2 - α'.

$$ \alpha = (\frac{\pi}{2} - \alpha') + 2k \pi \ \text{or} \ \alpha + (\frac{\pi}{2} - \alpha') = \pi + 2k \pi $$

This proves the formula for solving trigonometric equations of the form sin(α) = cos(α').

And so on.