Right Angle

A right angle is an angle that measures exactly 90 degrees or pi over two radians (π/2 rad).

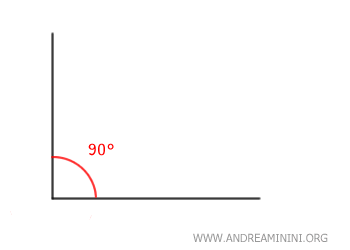
It's one of the most fundamental angles in geometry and is often represented by a small square at the vertex.

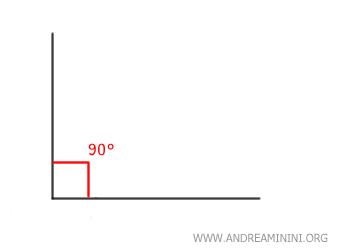
A right angle is formed when two lines intersect perpendicularly.

A right angle is half (1/2) of a straight angle (180°) and a quarter (1/4) of a full rotation (360°).

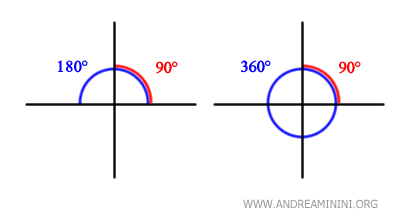
It is a key concept in many fields of mathematics, science, and engineering.

For instance, in architecture and engineering, perpendicularity is crucial for constructing stable buildings and structures. In mathematics, right angles are foundational in areas like trigonometry and Euclidean geometry. In physics, right angles are often used in vector problems, where decomposing a vector along perpendicular axes simplifies analysis.

Key Points About Right Angles

The right angle has several unique properties that make it important in many fields of mathematics and physics.

Here are some of its most significant properties:

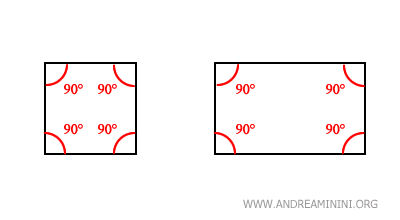
• Two perpendicular lines form four right angles.
  When two lines intersect to form a 90-degree angle, they are perpendicular and create four right angles.
  

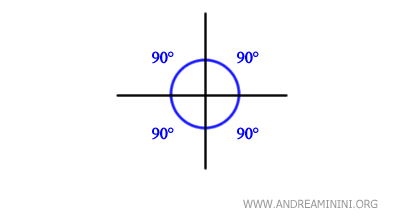
  This is evident in geometric figures like squares and rectangles, where four such angles can always be identified.
  

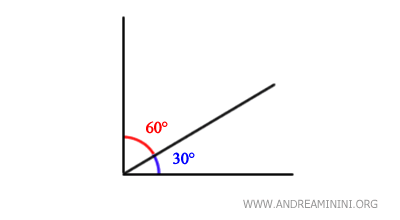
• Complementary Angles
  Two angles are called "complementary angles" if their measures add up to a right angle.
  
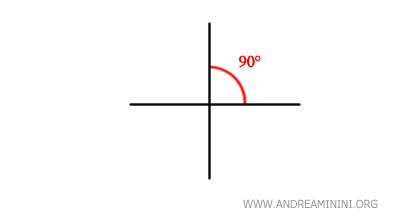
• Perpendicularity
  Two lines are perpendicular if they form a right angle where they meet. This property is fundamental in Euclidean geometry.
  
• Right Triangle
  In a right triangle, the right angle is the angle opposite the longest side, known as the hypotenuse.
• Pythagorean Theorem
  The Pythagorean theorem states that in a right triangle, the square of the hypotenuse's length is equal to the sum of the squares of the lengths of the other two sides. This is one of the most fundamental relationships in mathematics.

History

The right angle has been known since ancient times.

The ancient Egyptians used knotted ropes to create an "Egyptian triangle" with sides 3, 4, and 5, which is a classic example of a right triangle. They used this method to create right angles in construction.

The numbers 3, 4, and 5 also form a "Pythagorean triple".

Later, the ancient Greeks, particularly Euclid, developed a system of geometry known as Euclidean geometry, where the right angle plays a central role.

For example, the Pythagorean theorem is one of the most famous mathematical principles developed by the ancient Greeks and specifically pertains to right triangles, which have a right angle.

And so on.