Solving a Linear Equation with Sine and Cosine Using the Angle Sum Formula

A linear equation involving sine and cosine, $$ a \sin x + b \cos x + c = 0 $$, can be simplified using the angle sum formula, transforming it into the equivalent equation: $$ r \sin(x + k) + c = 0, $$ where the solution is: $$ \sin(x + k) = -\frac{c}{r}. $$

Here, \( r \) represents the amplitude of the sinusoidal wave:

$$ r = \sqrt{a^2 + b^2}, $$

and \( k \) is the phase shift, also known as the angle sum:

$$ k = \arctan \frac{b}{a}. $$

Note on signs. This method works seamlessly when both \( a \) and \( b \) are positive. However, if one or both coefficients are negative, it’s crucial to account for the signs of sine and cosine. You’ll need to determine the correct quadrant for the angle \( k \). While the tangent of the angle remains the same, the angle itself may belong to a different quadrant. Adjusting \( k \) according to the signs of \( a \) and \( b \) ensures accurate results.

Why use this method?

Transforming a linear equation with sine and cosine into an elementary trigonometric equation simplifies the solving process significantly.

A Practical Example

Let's solve the linear equation involving sine and cosine:

$$ \sqrt{3} \sin x + \cos x = \sqrt{3} $$

We can rewrite it as:

$$ \sqrt{3} \sin x + \cos x - \sqrt{3} = 0 $$

To tackle this, I’ll use the method of the supplementary angle:

$$ r \sin (x + k) + c = 0 $$

$$ \sqrt{a^2 + b^2} \sin (x + k) + c = 0 $$

Here, \( a = \sqrt{3} \), \( b = 1 \), and \( c = -\sqrt{3} \):

$$ \sqrt{(\sqrt{3})^2 + 1^2} \sin (x + k) - \sqrt{3} = 0 $$

$$ \sqrt{3 + 1} \sin (x + k) - \sqrt{3} = 0 $$

$$ \sqrt{4} \sin (x + k) - \sqrt{3} = 0 $$

$$ 2 \sin (x + k) - \sqrt{3} = 0 $$

The supplementary angle \( k \) is given by \( \arctan(b/a) \), which simplifies to \( k = \arctan(1/\sqrt{3}) \).

$$ 2 \sin \left(x + \arctan\left(\frac{1}{\sqrt{3}}\right)\right) - \sqrt{3} = 0 $$

Rearranging the terms:

$$ \sin \left(x + \arctan\left(\frac{1}{\sqrt{3}}\right)\right) = \frac{\sqrt{3}}{2} $$

Next, I multiply and divide inside the arctangent by \( \sqrt{3} \):

$$ \sin \left(x + \arctan\left(\frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}\right)\right) = \frac{\sqrt{3}}{2} $$

$$ \sin \left(x + \arctan\left(\frac{\sqrt{3}}{3}\right)\right) = \frac{\sqrt{3}}{2} $$

The tangent equals \( \sqrt{3}/3 \) at an angle of \( \pi/6 \) radians (or 30°).

So, the arctangent of \( \sqrt{3}/3 \) is \( \pi/6 \):

$$ \sin \left(x + \frac{\pi}{6}\right) = \frac{\sqrt{3}}{2} $$

This is a straightforward trigonometric equation with infinitely many solutions:

$$ x + \frac{\pi}{6} = \alpha + 2\pi k \vee x + \frac{\pi}{6} = (\pi - \alpha) + 2\pi k $$

where \( k \) is any integer.

Now, let’s determine the angle \( \alpha \).

For \( \alpha = x + \pi/6 \), \( \sin(\alpha) = \sqrt{3}/2 \) when \( \alpha = \pi/3 \) radians (or 60°).

$$ x + \frac{\pi}{6} = \frac{\pi}{3} + 2\pi k \vee x + \frac{\pi}{6} = \left(\pi - \frac{\pi}{3}\right) + 2\pi k $$

$$ x = \frac{\pi}{3} - \frac{\pi}{6} + 2\pi k \vee x = \pi - \frac{\pi}{3} - \frac{\pi}{6} + 2\pi k $$

$$ x = \frac{2\pi - \pi}{6} + 2\pi k \vee x = \frac{6\pi - 2\pi - \pi}{6} + 2\pi k $$

$$ x = \frac{\pi}{6} + 2\pi k \vee x = \frac{3\pi}{6} + 2\pi k $$

$$ x = \frac{\pi}{6} + 2\pi k \vee x = \frac{\pi}{2} + 2\pi k $$

When \( k = 0 \), the equation has two solutions: \( x = \pi/6 \) and \( x = \pi/2 \).

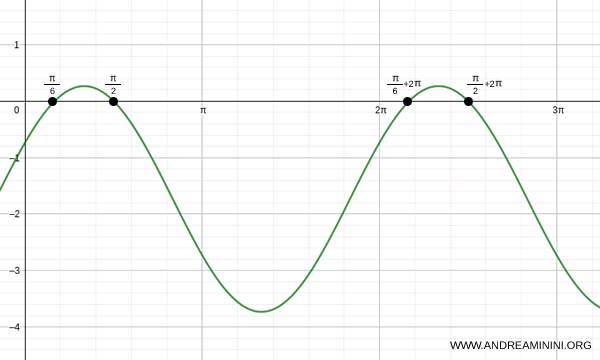
By varying \( k \), all other periodic solutions of the linear equation in sine and cosine can be determined.

Example 2

Let’s explore the linear equation involving sine and cosine:

$$ -\sqrt{3} \sin x + \cos x = \sqrt{3}, $$

which can be rewritten as:

$$ -\sqrt{3} \sin x + \cos x - \sqrt{3} = 0. $$

Here, the coefficients are \( a = -\sqrt{3} \), \( b = 1 \), and \( c = -\sqrt{3} \).

It’s important to note that the coefficient \( a < 0 \) is negative. Let’s examine how this impacts the solution process.

We’ll use the auxiliary angle method:

$$ r \sin (x + k) + c = 0, $$

where \( r = \sqrt{a^2 + b^2} \) and \( k = \arctan\left(\frac{b}{a}\right). \)

First, let’s calculate \( r \):

$$ r = \sqrt{(-\sqrt{3})^2 + 1^2} = \sqrt{3 + 1} = \sqrt{4} = 2. $$

Next, we determine the auxiliary angle \( k \):

$$ k = \arctan\left(\frac{1}{-\sqrt{3}}\right). $$

The tangent of \( k \) is \( -\frac{1}{\sqrt{3}} \), which corresponds to an angle of \( -\frac{\pi}{6} \) (or \( 330^\circ \)) in the fourth quadrant, where cosine is positive and sine is negative.

However, since \( a < 0 \) and \( b > 0 \), \( k \) must lie in the second quadrant, where sine is positive and cosine is negative, aligning with the signs of \( a \) and \( b \).

To correctly position \( k \) in the second quadrant, we add \( \pi \) to \( -\frac{\pi}{6} \):

$$ k = -\frac{\pi}{6} + \pi = \frac{5\pi}{6}. $$

Note: If \( k \) isn’t adjusted by adding \( \pi \), it would fall in the wrong quadrant, leading to incorrect results. Using \( k = -\frac{\pi}{6} \) (fourth quadrant) instead of \( k = \frac{5\pi}{6} \) (second quadrant) would produce a sinusoidal equation that doesn’t correctly reflect the signs of \( a \) and \( b \). This mismatch would result in an equation that differs from the original, ultimately yielding invalid solutions.

With \( k \) now correctly adjusted to \( \frac{5\pi}{6} \), we substitute it into the equation:

$$ 2 \sin\left(x + \frac{5\pi}{6}\right) - \sqrt{3} = 0. $$

Next, we isolate the sine term:

$$ \sin\left(x + \frac{5\pi}{6}\right) = \frac{\sqrt{3}}{2}. $$

This is a standard trigonometric equation of the form \( \sin(\alpha) = \text{number} \), which has infinitely many solutions:

$$ x + \frac{5\pi}{6} = \alpha + 2\pi k \quad \text{or} \quad x + \frac{5\pi}{6} = (\pi - \alpha) + 2\pi k, $$

where \( k \) is any integer.

Now, let’s find the angle \( \alpha \). Since \( \sin(\alpha) = \frac{\sqrt{3}}{2} \), we have \( \alpha = \frac{\pi}{3} \). Substituting this value into the solutions gives:

$$ x + \frac{5\pi}{6} = \frac{\pi}{3} + 2\pi k \quad \text{or} \quad x + \frac{5\pi}{6} = \pi - \frac{\pi}{3} + 2\pi k. $$

Simplifying these equations yields:

$$ x = \frac{\pi}{3} - \frac{5\pi}{6} + 2\pi k = -\frac{\pi}{2} + 2\pi k, $$

$$ x = \pi - \frac{\pi}{3} - \frac{5\pi}{6} + 2\pi k = \frac{\pi}{6} + 2\pi k. $$

Thus, the final solutions are:

$$ x = -\frac{\pi}{2} + 2\pi k \quad \text{and} \quad x = \frac{\pi}{6} + 2\pi k. $$

The graph below illustrates the first two solutions for \( k=0 \) and \( k=1 \):

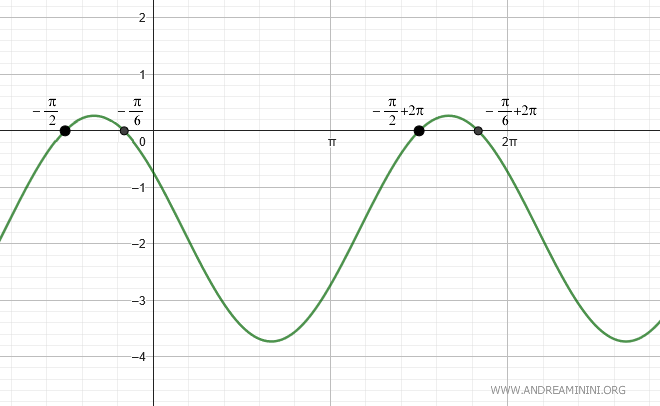
This example highlights the importance of considering the signs of \( a \) and \( b \) and correctly adjusting \( k \) to ensure it is placed in the correct quadrant, leading to accurate solutions.

The Proof

The auxiliary angle is a technique used to transform a linear trigonometric equation involving sine and cosine:

$$ y = a \sin x + b \cos x $$

into an equivalent sinusoidal equation:

$$ y = r \cdot \sin (x + k), $$

where \( r \) is the amplitude of the sinusoid:

$$ r = \sqrt{a^2+b^2}, $$

and \( k \) is the auxiliary angle, determined by the arctangent of the ratio \( b/a \):

$$ k = \arctan \frac{b}{a}. $$

Thus, a linear equation in sine and cosine:

$$ a \sin x + b \cos x + c = 0 $$

can be rewritten as:

$$ r \sin (x + k) + c = 0. $$

By isolating \( \sin(x + k) \):

$$ \sin (x + k) = -\frac{c}{r}, $$

we reduce it to a standard trigonometric equation \( \sin(\alpha) = \text{number} \), which can then be solved straightforwardly.

And so on.