Trigonometric Equation in the Form cot a = cot b
To solve the trigonometric equation $$ \cot \alpha = \cot \alpha' $$, we can use associated angles, converting cotangent into tangent: $$ \tan \left(\frac{\pi}{2} - \alpha\right) = \tan \left(\frac{\pi}{2} - \alpha'\right) $$. This follows the same approach as solving equations of the form tan x = tan y: $$ \left(\frac{\pi}{2} - \alpha\right) = \left(\frac{\pi}{2} - \alpha'\right) + k \pi $$.
A Practical Example
Let's solve this trigonometric equation:
$$ \cot \frac{1}{2} x + \frac{\pi}{2} = \cot \frac{5}{2} x - \frac{\pi}{2}$$
We convert cotangent to tangent on both sides:
$$ \tan \left( \frac{\pi}{2} - \frac{1}{2} x + \frac{\pi}{2} \right) = \tan \left( \frac{\pi}{2} - \frac{5}{2} x - \frac{\pi}{2} \right) $$
The tangent angles are:
$$ \alpha = \frac{\pi}{2} - \frac{1}{2} x + \frac{\pi}{2}$$
$$ \alpha' = \frac{\pi}{2} - \frac{5}{2} x - \frac{\pi}{2} $$
Now we apply the rule for equations where tan α = tan α' to find the values of x.
$$ \alpha = \alpha' + k \pi $$
In this case, α = π/2 - 1/2 x + 1/2 π and α' = π/2 - 5/2 x - 1/2 π
$$ \frac{\pi}{2} - \frac{1}{2} x + \frac{\pi}{2} = \frac{\pi}{2} - \frac{5}{2} x + k \pi - \frac{\pi}{2} $$
Next, we isolate x by simplifying:
$$ \frac{5}{2} x - \frac{1}{2} x = \frac{\pi}{2} - \frac{\pi}{2} + k \pi - \frac{\pi}{2} - \frac{\pi}{2} $$
$$ \frac{4}{2} x = k \pi - \pi $$
$$ 2 x = k \pi - \pi $$
$$ x = \frac{1}{2} (k \pi - \pi) $$
$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi $$
To find the solutions, we vary the integer k.
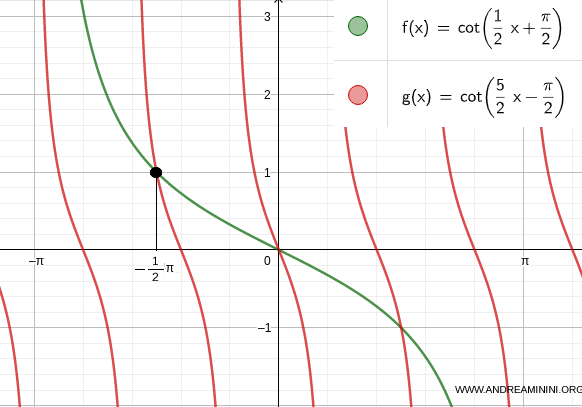
Checking for k = 0
$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi $$
$$ x = \frac{1}{2} (0) \pi - \frac{1}{2} \pi $$
$$ x = - \frac{1}{2} \pi $$
The first solution to the trigonometric equation is x = -1/2 π
Checking for k = 1
$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi $$
$$ x = \frac{1}{2} (1) \pi - \frac{1}{2} \pi $$
$$ x = \frac{1}{2} \pi - \frac{1}{2} \pi $$
$$ x = 0 $$
The second solution to the trigonometric equation is the trivial solution x = 0
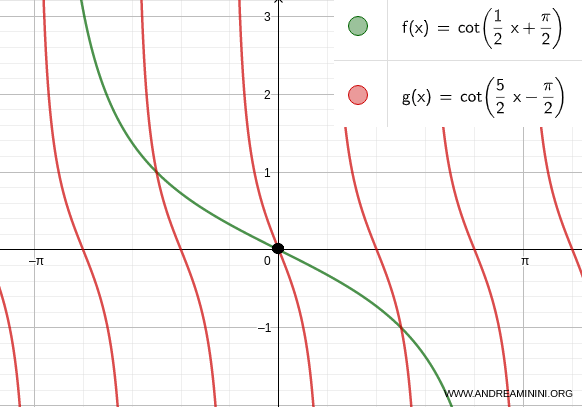
Checking for k = 2
$$ x = \frac{1}{2} k \pi - \frac{1}{2} \pi $$
$$ x = \frac{1}{2} (2) \pi - \frac{1}{2} \pi $$
$$ x = \pi - \frac{1}{2} \pi $$
$$ x = \frac{1}{2} \pi $$
The third solution to the trigonometric equation is x = 1/2 π
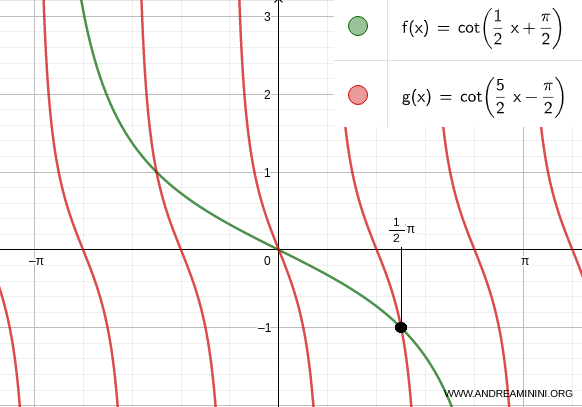
By adjusting k to 2, -2, 3, -3, etc., we can identify the infinite set of solutions for this equation.
The Proof
An inverse relationship exists between tangent and cotangent:
$$ \cot \alpha = \frac{1}{ \tan \alpha} $$
This means that cotangent is zero when tangent approaches positive or negative infinity, and vice versa.
Associated angles α and π/2 - α enable us to convert cotangent into tangent:
$$ \cot \alpha = \tan \left(\frac{\pi}{2} - \alpha\right) $$
Therefore, we can rewrite the trigonometric equation
$$ \cot \alpha = \cot \alpha' $$
in an equivalent form using the tangent of the associated angle π/2 - α:
$$ \tan \left(\frac{\pi}{2} - \alpha\right) = \tan \left(\frac{\pi}{2} - \alpha'\right) $$
Thus, the equation cot α = cot α' becomes a trigonometric equation of the form tan x = tan y, solved as:
$$ x = y + k \pi $$
where k is any integer, as both tangent and cotangent have a periodicity of π radians (180°).
In this case, the tangent arguments are x = π/2 - α and y = π/2 - α'
$$ \tan \left(\frac{\pi}{2} - \alpha\right) = \tan \left(\frac{\pi}{2} - \alpha'\right) + k \pi $$
This establishes the solution formula for the trigonometric equation cot α = cot α'.
And so on.
