Trigonometric Equation: tan(a) = -tan(b)

The trigonometric equation $$ \tan \alpha = - \tan \alpha' $$ can be solved using the formula $$ \tan \alpha = \tan (-\alpha') $$ which leads to the general solutions: $$ \alpha = (-\alpha') + k \pi $$ where k is any integer within the range (-∞, ∞).

The tangent is a periodic function with a period of π radians.

Therefore, the equation tan(α) = -tan(α') has infinitely many solutions, determined by integer multiples of the straight angle π.

A Practical Example

Let’s solve the trigonometric equation:

$$ \tan \frac{1}{2} x = - \tan \frac{3}{2} x $$

Since the tangent is an odd function, we can rewrite -tan(3/2x) as tan(-3/2x):

$$ \tan \frac{1}{2} x = \tan -\frac{3}{2} x $$

This transforms the equation into the standard form tan(α) = tan(α'):

$$ \alpha = \frac{1}{2} x $$ $$ \alpha' = -\frac{3}{2} x $$

Now, we can apply the general solution formula for a tan(α) = tan(α') equation:

$$ \alpha = \alpha' + k \pi $$

Substituting α and α' with the tangent arguments, we get:

$$ \frac{1}{2} x = (-\frac{3}{2} x) + k \pi $$

Rearranging to isolate the variable x:

$$ \frac{1}{2} x + \frac{3}{2} x = k \pi $$

$$ \frac{1+3}{2} x = k \pi $$

$$ \frac{4}{2} x = k \pi $$

$$ 2x = k \pi $$

$$ x = \frac{1}{2} k \pi $$

Thus, the equation has infinitely many solutions, where k is any integer.

To find specific solutions, we can assign different values to k.

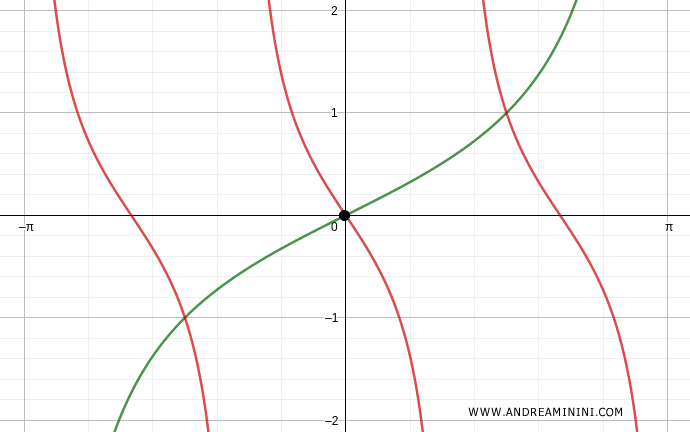
Verification for k=0

$$ x = \frac{1}{2} k \pi $$

$$ x = \frac{1}{2} (0) \pi $$

$$ x = 0 $$

The first solution is the trivial case x = 0.

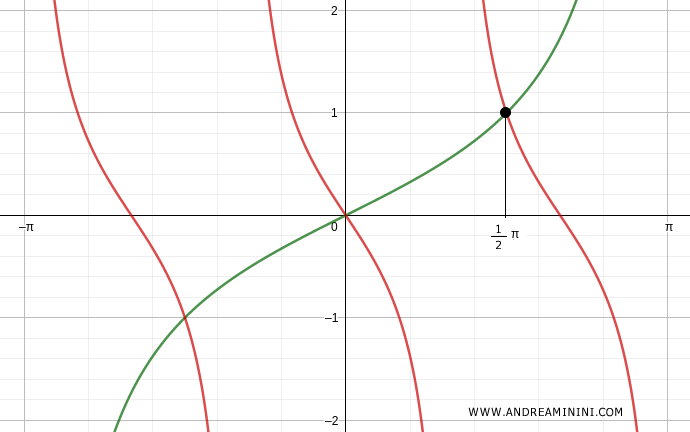
Verification for k=1

$$ x = \frac{1}{2} k \pi $$

$$ x = \frac{1}{2} (1) \pi $$

$$ x = \frac{1}{2} \pi $$

The second solution is x = 1/2π.

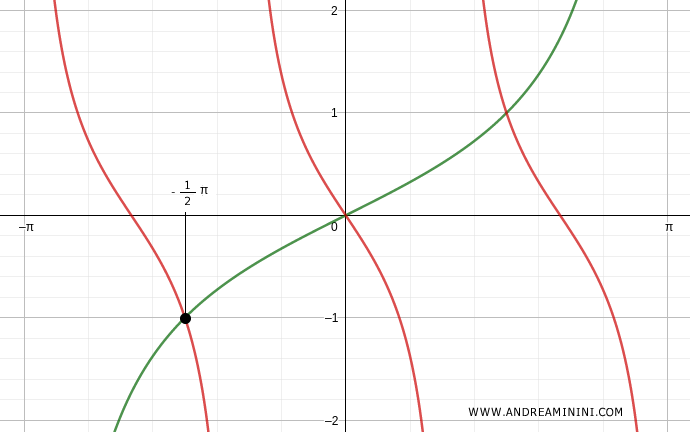
Verification for k=-1

$$ x = \frac{1}{2} k \pi $$

$$ x = \frac{1}{2} (-1) \pi $$

$$ x = -\frac{1}{2} \pi $$

The third solution is x = -1/2π.

By continuing with k = 2, -2, 3, ..., we can identify the remaining infinite solutions of the equation.

The Proof

The tangent is an odd function:

$$ -\tan \alpha = \tan (-\alpha) $$

Graphically:

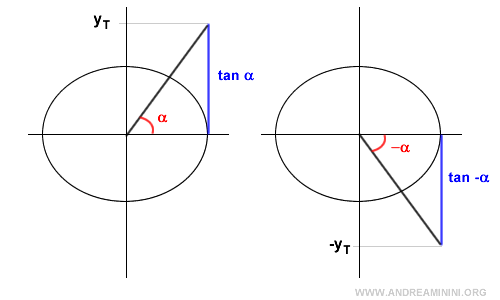
Thus, a trigonometric equation involving the tangent -tan(α'):

$$ \tan \alpha = -\tan \alpha' $$

can be rewritten equivalently as:

$$ \tan \alpha = \tan (-\alpha') $$

This allows us to solve the equation as a tan(α) = tan(α') problem:

$$ \alpha = \alpha' + k \pi $$

where k is any integer, and π radians (180°) corresponds to the periodicity of the tangent function.

In this case, the argument of the tangent is the opposite angle -α':

$$ \alpha = (-\alpha') + k \pi $$

This establishes the formula for solving the trigonometric equation.

And so forth.