Trigonometric Equation of the Form sin(α) = -sin(α')

The trigonometric equation $$ \sin \alpha = - \sin \alpha' $$ can be solved using the formula $$ \sin \alpha = \sin(- \alpha' ) $$, which leads to the solutions: $$ α = (-α') + 2k \pi \ ∨ \ α+(-α') = \pi + 2k \pi $$

Example

Let’s solve the trigonometric equation:

$$ \sin(\frac{1}{2}x) = - \sin(\frac{1}{6}x) $$

Since the sine function is an odd function, we can rewrite the equation by recognizing that -sin(1/6x) = sin(-1/6x):

$$ \sin(\frac{1}{2}x) = \sin(-\frac{1}{6}x) $$

This transforms the equation into the standard form sin(α) = sin(α'), where:

$$ \alpha = \frac{1}{2}x \\ \alpha' = -\frac{1}{6}x $$

Using the formula for solving sin(α) = sin(α'), we have:

$$ α = α' + 2k \pi \ ∨ \ α+α' = \pi + 2k \pi $$

Substituting the expressions for α and α', and isolating x, we obtain:

$$ \frac{1}{2}x = -\frac{1}{6}x + 2k \pi \ ∨ \ \frac{1}{2}x + (-\frac{1}{6}x) = \pi + 2k \pi $$

Simplifying:

$$ \frac{1}{2}x + \frac{1}{6}x = 2k \pi \ ∨ \ \frac{1}{2}x -\frac{1}{6}x = \pi + 2k \pi $$

$$ \frac{4}{6}x = 2k \pi \ ∨ \ \frac{2}{6}x = \pi + 2k \pi $$

$$ \frac{2}{3}x = 2k \pi \ ∨ \ \frac{1}{3}x = \pi + 2k \pi $$

Therefore:

$$ x = \frac{3}{2} \cdot 2k \pi \ ∨ \ x = 3 \cdot ( \pi + 2k \pi ) $$

$$ x = 3k \pi \ ∨ \ x = 3 \pi + 6k \pi $$

We have found an infinite number of solutions, where k is any integer (positive, negative, or zero).

Let’s examine the solutions for k=0:

$$ x = 3(0) \pi \ ∨ \ x = 3 \pi + 6(0) \pi $$

$$ x = 0 \ ∨ \ x = 3 \pi $$

When k=0, the trigonometric equation has two solutions: x=0 and x=3π.

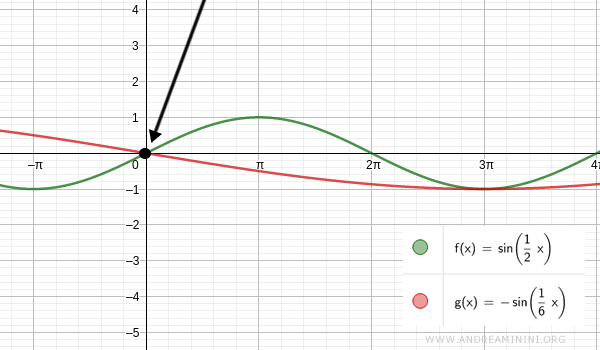
The first solution, x=0, is straightforward:

$$ \sin(\frac{1}{2}x) = - \sin(\frac{1}{6}x) $$

$$ \sin(\frac{1}{2} \cdot 0) = - \sin(\frac{1}{6} \cdot 0) $$

$$ \sin(0) = \sin(0) $$

$$ 0 = 0 $$

This means the two functions are equal at the origin (x=0).

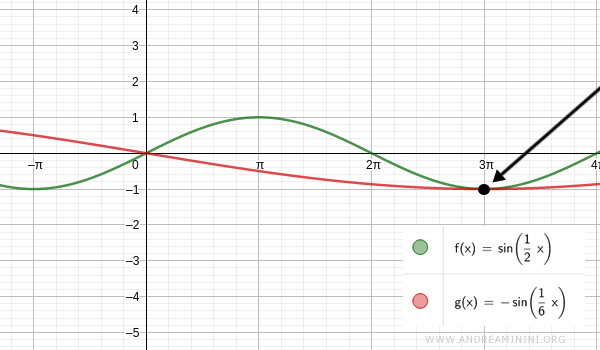
The second solution is x=3π:

$$ \sin(\frac{1}{2}x) = - \sin(\frac{1}{6}x) $$

$$ \sin(\frac{1}{2} \cdot 3 \pi) = - \sin(\frac{1}{6} \cdot 3 \pi) $$

$$ \sin(\frac{3}{2} \pi) = - \sin(\frac{1}{2} \pi) $$

$$ -1 = -1 $$

The two functions are also equal for x=3π.

All other infinite solutions can be found by substituting different integer values for k, such as k=-1, k=2, k=-2, k=3, and so on.

 

The Proof

The sine function is an odd function:

$$ \sin(-\gamma) = -\sin(\gamma) $$

Therefore, the trigonometric equation:

$$ \sin \alpha = -\sin(\alpha') $$

can be rewritten equivalently by replacing -sin(α') with sin(-α'):

$$ \sin \alpha = \sin(-\alpha') $$

This reduces the problem to solving a standard sin(α) = sin(α') equation:

$$ α = α' + 2k \pi \ ∨ \ α+α' = \pi + 2k \pi $$

Using the opposite angle -α':

$$ α = (-α') + 2k \pi \ ∨ \ α+(-α') = \pi + 2k \pi $$

And so on.