Second-Degree Equations in Sine and Cosine

A second-degree equation involving sine and cosine takes the form: $$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d $$

How to Solve Second-Degree Sine and Cosine Equations

Second-degree equations can be solved using different methods, depending on whether they are homogeneous or not.

Method 1: Homogeneous Equation

If the trigonometric equation is homogeneous (i.e., the constant term is zero) and the coefficient \( a \) is also zero, the equation simplifies to:

$$ b \sin x \cos x + c \cos^2 x = 0$$

From here, you can factor out \( \cos x \):

$$ \cos x (b \sin x + c \cos x) = 0 $$

Then apply the zero-product property to find when either \( \cos x \) or \( b \sin x + c \cos x \) equals zero.

Note: This method also works for homogeneous equations where \( c = 0 \). $$ a \sin^2 x + b \sin x \cos x = 0 $$ In this case, factor out \( \sin x \): $$ \sin x (a \sin x + b \cos x) = 0 $$ Then, as before, solve using the zero-product property to find the solutions.

Method 2: Homogeneous Equation

To solve a homogeneous second-degree equation in sine and cosine, divide through by \( \cos^2 x \):

$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = 0$$

$$ \frac{a \sin^2 x + b \sin x \cos x + c \cos^2 x}{\cos^2 x} = 0 $$

$$ \frac{a \sin^2 x}{\cos^2 x} + \frac{b \sin x \cos x}{\cos^2 x} + \frac{c \cos^2 x}{\cos^2 x} = 0 $$

$$ a \frac{\sin^2 x}{\cos^2 x} + b \frac{\sin x}{\cos x} + c = 0 $$

Now use the second fundamental trigonometric identity to replace \( \sin x / \cos x \) with \( \tan x \):

$$ a \tan^2 x + b \tan x + c = 0 $$

At this point, substitute \( y = \tan x \) to turn the equation into a standard quadratic equation:

$$ a y^2 + b y + c = 0 $$

Solve the quadratic equation using the standard formula:

$$ y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

Once you find the solutions \( y_1 \) and \( y_2 \) (if they exist), solve for \( x \) by addressing the corresponding basic trigonometric equations:

$$ \tan x = y_1 $$

$$ \tan x = y_2 $$

This approach simplifies the original second-degree equation into basic trigonometric equations.

Method 3: Non-Homogeneous Equation

If the equation is non-homogeneous, meaning the constant term \( d \neq 0 \), it looks like this:

$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d $$

You can rewrite it as an equivalent homogeneous equation by multiplying the constant term by 1:

$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d \cdot 1 $$

Using the first fundamental trigonometric identity, \( \sin^2 x + \cos^2 x = 1 \), substitute 1 with \( \sin^2 x + \cos^2 x \):

$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x = d (\sin^2 x + \cos^2 x) $$

$$ a \sin^2 x + b \sin x \cos x + c \cos^2 x - d (\sin^2 x + \cos^2 x) = 0 $$

This transforms the equation into a homogeneous one, which can be solved using one of the earlier methods (Method 1 or Method 2).

A Practical Example

Example 1

I need to solve the second-degree homogeneous equation in sine and cosine:

$$ \sin^2 x - \sqrt{3} \sin x \cos x = 0 $$

Since the coefficient of cosine squared is zero, I’ll solve this equation using the zero-product property.

I factor out the sine function:

$$ \sin x (\sin x - \sqrt{3} \cos x) = 0 $$

Next, I determine when each factor equals zero:

• The equation \(\sin x = 0\) is a basic sine equation: $$ \sin x = 0 $$ In this case, the solution is straightforward. The equation is satisfied when \( x = 0 + k\pi \). Therefore, the first solution to the second-degree equation is \( x = 0 + k\pi \).
  

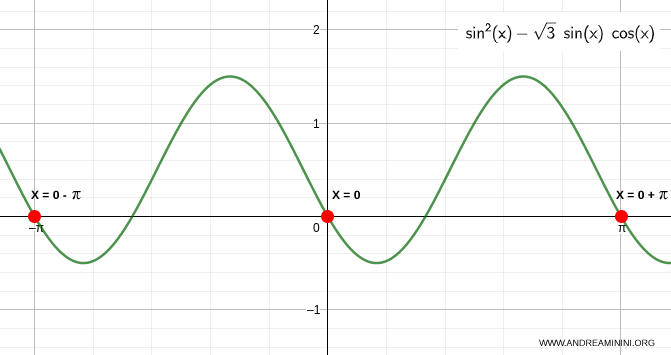
• The equation \(\sin x - \sqrt{3} \cos x = 0\) is a linear trigonometric equation. I’ll solve it using standard techniques for linear trigonometric equations: $$ \sin x - \sqrt{3} \cos x = 0 $$ Dividing through by cosine: $$ \frac{\sin x}{\cos x} - \sqrt{3} = 0 $$ $$ \tan x = \sqrt{3} $$ This is a basic tangent equation, which is satisfied when \( x = \pi/3 + k\pi \). Hence, the second solution to the second-degree equation is \( x = \pi/3 + k\pi \).
  

 

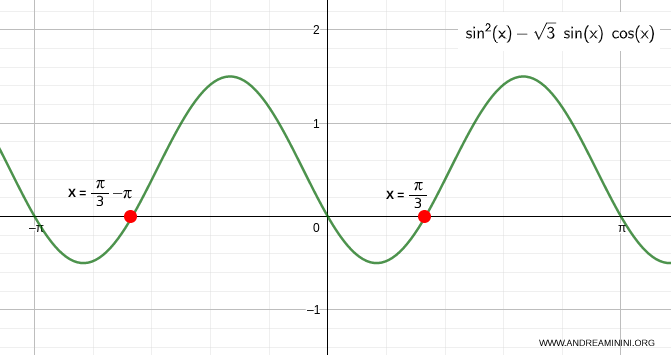
Therefore, the solutions to the second-degree equation in sine and cosine are:

$$ x = 0 + k \pi \ \ \text{or} \ \ \frac{\pi}{3} + k \pi $$

Example 2

Now I’ll solve the second-degree equation in sine and cosine:

$$ \sin^2 x + 2 \sin x \cos x - \cos^2 x = 0 $$

This is a homogeneous equation.

Since all coefficients are non-zero, I’ll use the substitution method (Technique 2).

Dividing through by \(\cos^2 x\):

$$ \frac{\sin^2 x + 2 \sin x \cos x - \cos^2 x}{\cos^2 x} = \frac{0}{\cos^2 x} $$

$$ \frac{\sin^2 x}{\cos^2 x} + 2 \frac{\sin x}{\cos x} - 1 = 0 $$

Using the fundamental trigonometric identity, \(\sin x / \cos x = \tan x\):

$$ \tan^2 x + 2 \tan x - 1 = 0 $$

This reduces the equation to a quadratic in a single trigonometric function.

Let \( y = \tan x \):

$$ y^2 + 2y - 1 = 0 $$

Solving the quadratic equation:

$$ y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

$$ y = \frac{-2 \pm \sqrt{4 + 4}}{2} $$

$$ y = \frac{-2 \pm \sqrt{8}}{2} $$

$$ y = -1 \pm \sqrt{2} $$

Thus, the solutions are:

$$ y = \begin{cases} -1 + \sqrt{2} \\ -1 - \sqrt{2} \end{cases} $$

Since \( y = \tan x \), this translates to:

$$ \tan x = \begin{cases} -1 + \sqrt{2} \\ -1 - \sqrt{2} \end{cases} $$

To find \( x \), I compute the arctangent of each value:

$$ x = \begin{cases} \arctan(-1 + \sqrt{2}) \\ \arctan(-1 - \sqrt{2}) \end{cases} $$

The solutions can be expressed as \( x = \pi/8 + k\pi/2 \), where \( k \) is any integer.

Graphically, this can be represented as:

 

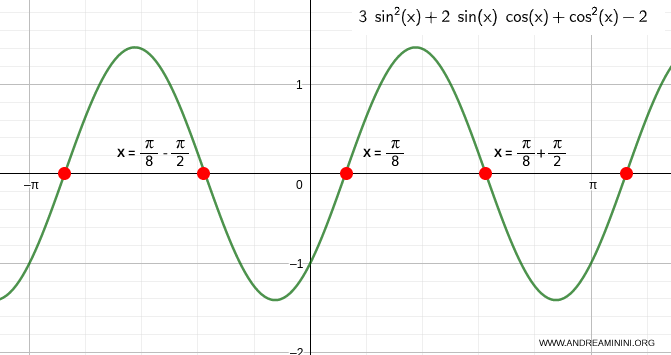
Example 3

Finally, I’ll solve the second-degree equation in sine and cosine:

$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 x = 2 $$

This is a non-homogeneous equation.

To solve it, I first convert it into a homogeneous equation using Technique 3:

$$ 3 \sin^2 x + 2 \sin x \cos x + \cos^2 x = 2 (\sin^2 x + \cos^2 x) $$

Simplifying:

$$ \sin^2 x + 2 \sin x \cos x - \cos^2 x = 0 $$

This results in an equivalent homogeneous equation.

I can now solve it using the techniques described for homogeneous equations.

Note: The steps for this solution are identical to those in Example 2, so they will not be repeated here.