Basis Theorem in the Topology Induced by a Metric

In a metric space $(X, d)$, the collection of open balls $$ \mathcal{B} = \{B_d(x, \varepsilon) \mid x \in X, \varepsilon > 0\} $$ forms a basis for a topology on $X$.

A collection of open sets $\mathcal{B}$ is a basis for a topology if every open set in the topology can be expressed as a union of sets from the basis.

Moreover, a collection $\mathcal{B}$ is considered a basis if it satisfies the following two conditions:

For every point $x \in X$, there is at least one set $B \in \mathcal{B}$ such that $x \in B$. (Covering)
If $x \in B_1 \cap B_2$ for two sets $B_1, B_2 \in \mathcal{B}$, then there exists a set $B_3 \in \mathcal{B}$ such that $x \in B_3 \subseteq B_1 \cap B_2$. (Intersection compatibility)

The theorem states that the collection of all open balls $B_d(x, \varepsilon)$ satisfies these two conditions, and as such, can be used to define a topology on $X$.

An open ball is the set of all points $y \in X$ such that the distance between $x$ and $y$ is less than $\varepsilon$ for any positive number $\varepsilon$: $$ B_d(x, \varepsilon) = \{y \in X \mid d(x, y) < \varepsilon\}. $$

In simpler terms, this theorem shows that the topological structure of a metric space can be fully described using open balls.

An Example
Proof

An Example

Let’s look at an open set $A$ in the plane $\mathbb{R}^2$, defined as follows:

$$ A = \{(x_1, x_2) \in \mathbb{R}^2 \mid 1 < x_1^2 + x_2^2 < 4 \} $$

Geometrically, this set represents a ring in the plane, with an inner radius of 1 and an outer radius of 2.

It’s an open set because it excludes the boundaries of the circles with radii 1 and 2.

example

How can $A$ be written as a union of open balls?

According to the basis theorem, $A$ can be expressed as a union of open balls.

For example, we can take several open balls centered at points within the ring, each with a radius small enough to fit entirely inside the ring.

Consider the open ball centered at the point $p_1 = (1.5, 0)$ with radius $\varepsilon_1 = 0.3$, that is:

$$ B1_d((1.5, 0), 0.3) = \{(x_1, x_2) \in \mathbb{R}^2 \mid d((1.5, 0), (x_1, x_2)) < 0.3\} $$

This ball is entirely contained within the ring $A$.

example

Next, consider the open ball centered at the point $p_2 = (-1.5, 0)$ with radius $\varepsilon_2 = 0.4$:

$$ B2_d((-1.5, 0), 0.4) = \{(x_1, x_2) \in \mathbb{R}^2 \mid d((-1.5, 0), (x_1, x_2)) < 0.4\} $$

This ball is also completely within the ring $A$.

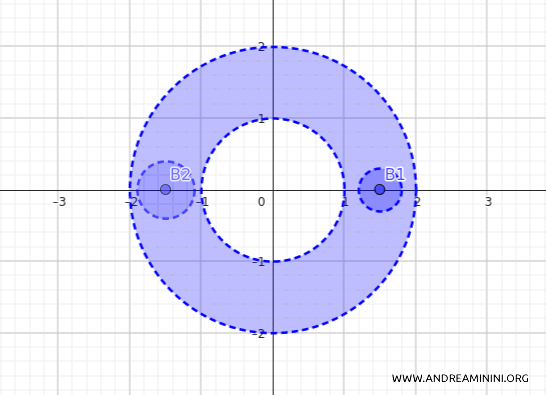
example

Continuing this process, we can construct many more open balls, centered at different points inside the ring, all with small enough radii to remain entirely within $A$.

The key point is that we can cover the entire set $A$ with a union of these open balls, leaving no "gaps" or empty spaces.

Formally, we can write:

$$ A = \bigcup_{i} B_d(x_i, \varepsilon_i) $$

Where $x_i$ are the centers of various open balls and $\varepsilon_i$ are their radii.

Each $B_d(x_i, \varepsilon_i)$ is an open ball centered at $x_i$ with radius $\varepsilon_i$ such that the ball is contained in $A$.

This example demonstrates how any open set (such as the ring $A$) in $\mathbb{R}^2$ can be written as a union of open balls.

In other words, open balls are the "building blocks" that, when combined, describe the structure of open sets in a metric-induced topology.

Proof

The aim of the proof is to show that the collection of open balls in a metric space $(X, d)$ forms a basis for a topology on $X$.

We do this by checking whether the conditions for being a basis are fulfilled:

1] The first condition states that every point in the space must belong to an open ball

This is easy to verify: for any point $x \in X$, we can take the open ball $B_d(x, \varepsilon)$ centered at $x$ with radius $\varepsilon > 0$.

Clearly, the point $x$ belongs to $B_d(x, \varepsilon)$ for any $\varepsilon > 0$.

Therefore, the collection of open balls satisfies the first condition for being a basis, as every point in $X$ is contained in at least one open ball.

2] The second condition requires that if a point $x$ belongs to the intersection of two open balls $x \in B_1 \cap B_2$, then there must be a smaller open ball $B_3$ centered at $x$ that is entirely contained within the intersection $B_1 \cap B_2$.

This is crucial because it ensures we can "refine" the open balls around $x$ and always find a smaller covering that respects the topology.

Let $B_1$ and $B_2$ be two open balls in $\mathcal{B}$ (the collection of all open balls).

Assume $x \in B_1 \cap B_2$. Therefore, $x$ belongs to both $B_1$ and $B_2$.

We need to find an open ball $B_3$ centered at $x$ such that $B_3$ is entirely contained within $B_1 \cap B_2$.

If the point $x$ is in the open ball $B_1$, we can always find a smaller open ball centered at $x$ that is entirely within $B_1$, and the same applies for $B_2$.

For $B_1$, there exists an open ball centered at $x$ with a certain radius $\delta_1$ such that $B_d(x, \delta_1) \subseteq B_1$.
For $B_2$, there exists an open ball centered at $x$ with a certain radius $\delta_2$ such that $B_d(x, \delta_2) \subseteq B_2$.

To obtain an open ball contained in both $B_1$ and $B_2$, we take the open ball centered at $x$ with radius $\delta = \min\{\delta_1, \delta_2\}$, which is the smaller of the two radii.

This ball $B_d(x, \delta)$ will be contained in both $B_1$ and $B_2$, and therefore, it will be contained in $B_1 \cap B_2$.

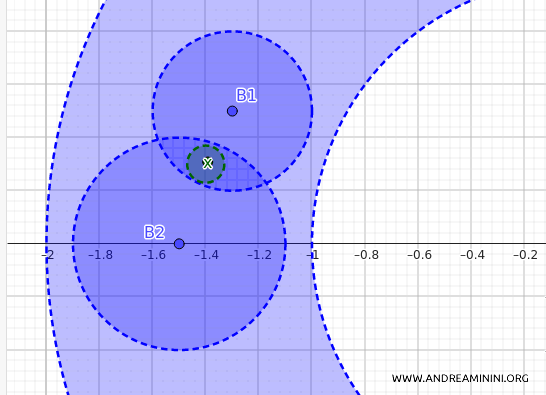
example

The second condition for being a basis is also satisfied.

In conclusion, I have demonstrated that the collection of open balls meets both conditions required to be a basis.

As a result, the collection of open balls forms a basis for a topology on $X$, known as the topology induced by the metric.

And so forth.