How to Derive the Equation of a Circle from Its Radius and Center
The equation of a circle in the Cartesian plane can be derived if you know the radius (r) and the coordinates of the center, C(x0, y0). The formula is: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
This equation represents all the points \((x, y)\) that are at a distance \(r\) from the center \((x_0, y_0)\).
Practical Example
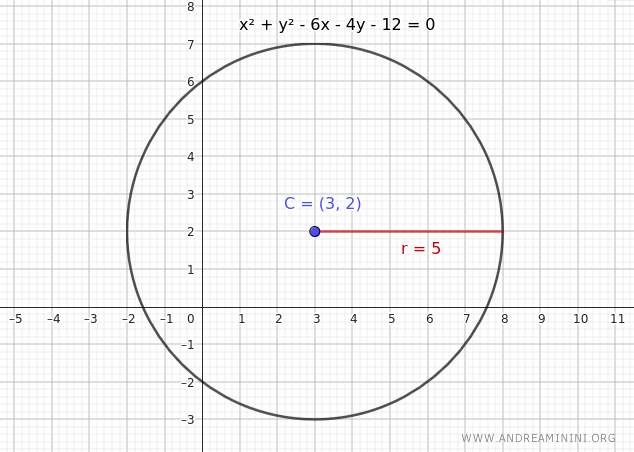
Let's consider a circle with center \( C(3, 2) \) and radius \( r = 5 \).
To find the equation of the circle, we use the formula:
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
Here, the center coordinates are x0=3 and y0=2, and the radius is r=5
$$ (x - 3)^2 + (y - 2)^2 = 5^2 $$
$$ (x - 3)^2 + (y - 2)^2 = 25 $$
The equation \((x - 3)^2 + (y - 2)^2 = 25\) represents all points \((x, y)\) that are 5 units away from the center \((3, 2)\).
To convert this equation to the general form, we expand both binomials:
$$ (x - 3)^2 + (y - 2)^2 = 25 $$
$$ x^2 - 6x + 9 + y^2 -4y + 4 - 25 = 0 $$
$$ x^2 + y^2 - 6x - 4y - 12 = 0 $$
This is a practical example of how to determine the equation of a circle given the center and radius.
Note: To verify if a point lies on the circle, simply substitute the coordinates of the point into the equation and check if it holds true. For instance, to verify if the point P(6,6) is on the circle, substitute x=6 and y=6 into the equation. $$ (x - 3)^2 + (y - 2)^2 = 25 $$ $$ (6 - 3)^2 + (6 - 2)^2 = 25 $$ $$ 3^2 + 4^2 = 25 $$ $$ 9 + 16 = 25 $$ $$ 25 = 25 $$ Since the distance equals the radius, the point (6,6) lies on the circle, confirming that the equation is correct. Alternatively, you can substitute x=6 and y=6 into the general equation of the circle. The result will be the same. $$ x^2 + y^2 - 6x - 4y - 12 = 0 $$ $$ 6^2 + 6^2 - 6 \cdot 6 - 4 \cdot 6 - 12 = 0 $$ $$ 36 + 36 - 36 - 24 - 12 = 0 $$ $$ 0 = 0 $$
Proof
Initially, we know the center of the circle: \(C(x_0, y_0)\) and the radius: \(r\).
We need to prove that the equation of the circle in the Cartesian plane is \((x - x_0)^2 + (y - y_0)^2 = r^2\).
By definition, a circle is the set of all points in a plane that are equidistant from a fixed point, called the center. The constant distance is the radius \(r\).
Thus, if we take any point \(P(x, y)\) on the circle, the distance between \(P(x, y)\) and the center \(C(x_0, y_0)\) must equal the radius \(r\).
The distance formula between two points \((x, y)\) and \((x_0, y_0)\) in the Cartesian plane is:
$$ d = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$
In this case, the distance (d) must be equal to the radius (r) of the circle, so d=r.
$$ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r $$
To eliminate the square root, square both sides of the equation:
$$ (\sqrt{(x - x_0)^2 + (y - y_0)^2})^2 = r^2 $$
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
This equation represents all points \((x, y)\) that are at a distance \(r\) from the center \(C(x_0, y_0)\).
Thus, we have proven the formula for the equation of a circle given the center \(C(x_0, y_0)\) and the radius \(r\).
