The Equation of a Circle Passing Through Three Non-Collinear Points

To find the equation of a circle that passes through three non-collinear points \( P(x_1, y_1) \), \( Q(x_2, y_2) \), and \( R(x_3, y_3) \), we need to solve the following system of equations for the coefficients "a," "b," and "c": $$ \begin{cases} x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 \\ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 \\ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 \end{cases} $$ Once the coefficients "a," "b," and "c" are determined, they are substituted into the general equation of the circle: $$ x^2 + y^2 + ax + by + c = 0 $$

A Practical Example

Let's consider the following points on the plane:

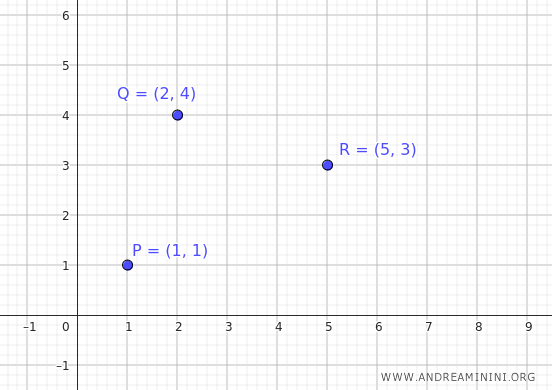
$$ P(1, 1) $$

$$ Q(2, 4) $$

$$ R(5, 3) $$

These are three non-collinear points on the Cartesian plane.

The general equation of the circle is:

$$ x^2 + y^2 + ax + by + c = 0 $$

To solve this problem, follow these steps:

1] Write the equations for each point

Substitute the coordinates of the points into the system of equations:

• For point P(1,1), substitute x=1 and y=1:
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 1^2 + 1^2 + a \cdot 1 + b \cdot 1 + c = 0 $
  $ 1 + 1 + a + b + c = 0 $
  $ a + b + c = -2 $
• For point Q(2, 4), substitute x=2 and y=4:
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 2^2 + 4^2 + a \cdot 2 + b \cdot 4 + c = 0 $
  $ 4 + 16 + 2a + 4b + c = 0 $
  $ 2a + 4b + c = -20 $
• For point R(5, 3), substitute x=5 and y=3:
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 5^2 + 3^2 + a \cdot 5 + b \cdot 3 + c = 0 $
  $ 25 + 9 + 5a + 3b + c = 0 $
  $ 5a + 3b + c = -34 $

2] Construct and solve the system of equations

Combine the three equations into the following system of linear equations:

$$ \begin{cases} a + b + c = -2 \\ 2a + 4b + c = -20 \\ 5a + 3b + c = -34 \\ \end{cases} $$

This system allows us to find the coefficients "a," "b," and "c" that satisfy the three circle equations simultaneously.

Next, solve the system using any method of your choice.

In this case, I choose the reduction method.

Subtract the first equation from the second:

$$ \begin{cases} a + b + c = -2 \\ (2a + 4b + c) - (a + b + c) = -20 - (-2) \\ 5a + 3b + c = -34 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 5a + 3b + c = -34 \\ \end{cases} $$

Subtract the first equation from the third:

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ (5a + 3b + c) - (a + b + c) = -34 - (-2) \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 4a + 2b = -32 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 2a + b = -16 \\ \end{cases} $$

By eliminating "c" from the last two equations, we get a simpler system to determine the values of "a" and "b".

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 2a + b = -16 \\ \end{cases} $$

Multiply the third equation by 3:

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 3 \cdot (2a + b) = 3 \cdot ( -16) \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 6a + 3b = -48 \\ \end{cases} $$

Now subtract the second equation from the third:

This eliminates the variable "b" and gives us the value of "a".

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 6a + 3b - (a + 3b) = -48 - (-18) \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ (6a - a) + (3b - 3b) = -48 + 18 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 5a = -30 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ a = - \frac{30}{5} \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ a = - 6 \\ \end{cases} $$

After finding the value of \( a = -6 \), substitute it back into the other equations.

$$ \begin{cases} -6 + b + c = -2 \\ -6 + 3b = -18 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} b + c = -2 + 6 \\ 3b = -18 + 6 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} b + c = 4 \\ b = - \frac{12}{3} \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} b + c = 4 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

Now we have found the value of \( b = -4 \). Substitute this into the first equation.

$$ \begin{cases} -4 + c = 4 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} c = 4 + 4 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} c = 8 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

3] Write the equation of the circle passing through the three points

We have found the three coefficients: a = -6, b = -4, and c = 8.

Therefore, the equation of the circle passing through the points P, Q, and R is:

$$ x^2 + y^2 + ax + by + c = 0 $$

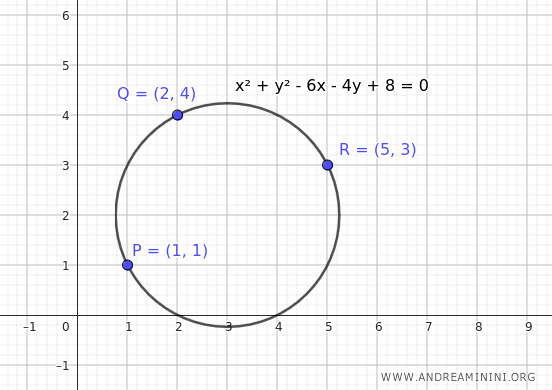
$$ x^2 + y^2 - 6x - 4y + 8 = 0 $$

Here is the graph of the circle:

The Proof

The equation of the circle is given in the form:

$$ x^2 + y^2 + ax + by + c = 0 $$

To ensure the circle passes through the points \( P \), \( Q \), and \( R \), the coordinates of each point must satisfy this equation.

• Point P(x₁,y₁): $$ x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 $$
• Point Q(x₂,y₂): $$ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 $$
• Point R(x₃,y₃): $$ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 $$

The coefficients "a," "b," and "c" are the same in all equations.

Therefore, we can construct a system of equations:

$$ \begin{cases} x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 \\ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 \\ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 \\ \end{cases} $$

At this point, solve the system of equations to find the coefficients \( a \), \( b \), and \( c \), which define the circle passing through the given points.

Once obtained, substitute them into the general equation of the circle:

$$ x^2 + y^2 + ax + by + c = 0 $$

And so forth.