External Circles
Two circles are considered external if the distance between their centers, denoted as OO', is greater than the sum of their radii: $$ \overline{OO'} > r + r' $$. This means the circles do not touch or overlap at any point.
In this context, OO' indicates the distance between the centers of the two circles, and r and r' represent their respective radii.
Graphically, this means that each circle lies entirely outside the other, with no points in common.
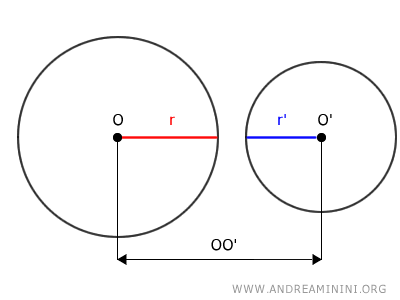
When the distance OO' is greater than the sum of the radii r + r', each center, O and O', lies outside the circumference of the other circle.
Moreover, the sum of the radius and the center of one circle (O + r and O' + r') cannot intersect the other circle, ensuring the two circles remain entirely separate.
A Practical Example
Let's determine if the two circles defined by the following equations are external to each other:
$$ C_1 : x^2 + y^2 - 4x - 8y = -16 $$
$$ C_2 : x^2 + y^2 - 2x + 4y = 2 $$
First, I'll rewrite the equations in standard form $ (x - h)^2 + (y - k)^2 = r^2 $ to find the center $ (h, k) $ and the radius $ r $ of each circle:
- First equation: $$ x^2 + y^2 - 4x - 8y = -16 $$ Completing the square for \(x\) and \(y\) by adding and subtracting the necessary terms: $$ (x^2 - 4x + 4) + (y^2 - 8y + 16) = -16 + 4 + 16 $$ $$ (x - 2)^2 + (y - 4)^2 = 4 $$ Thus, the first circle has center \((2, 4)\) and radius \(r_1 = \sqrt{4} = 2\).
- Second equation: $$ x^2 + y^2 - 2x + 4y = 2 $$ Completing the square for \(x\) and \(y\): $$ (x^2 - 2x + 1) + (y^2 + 4y + 4) = 2 + 1 + 4 $$ $$ (x - 1)^2 + (y + 2)^2 = 7 $$ Thus, the second circle has center \((1, -2)\) and radius \(r_2 = \sqrt{7} \approx 2.65\).
Next, I calculate the distance between the centers of the circles using the Euclidean distance formula:
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
The center of the first circle is \(O_1 = (2, 4)\), so x1 = 2 and y1 = 4. The center of the second circle is \(O_2 = (1, -2)\), so x2 = 1 and y2 = -2.
$$ d = \sqrt{(1 - 2)^2 + (-2 - 4)^2} $$
$$ d = \sqrt{(-1)^2 + (-6)^2} $$
$$ d = \sqrt{1 + 36} $$
$$ d = \sqrt{37} \approx 6.08 $$
Finally, I check whether the circles are external to each other.
The circles are external if the distance between their centers is greater than the sum of their radii:
$$ d > r_1 + r_2 $$
$$ 6.08 > 2 + 2.65 $$
$$ 6.08 > 4.65 $$
Since \( 6.08 > 4.65 \), the two circles are external and do not intersect or touch.
Alternative Solution
We need to determine if the two circles are external to each other:
$$ C_1 : x^2 + y^2 - 4x - 8y = -16 $$
$$ C_2 : x^2 + y^2 - 2x + 4y = 2 $$
We use this formula to find the center of each circle, \( ( - \frac{a}{2}, - \frac{b}{2} ) \), considering the circle equation in the form \( x^2 + y^2 + ax + by + c = 0 \):
$$ C_1 : x^2 + y^2 - 4x - 8y + 16 = 0 $$
$$ C_2 : x^2 + y^2 - 2x + 4y - 2 = 0 $$
For the first circle, the coefficients are a = -4 and b = -8.
$$ O_1 = \left( - \frac{a}{2}, - \frac{b}{2} \right) = \left( - \frac{-4}{2}, - \frac{-8}{2} \right) = (2, 4) $$
For the second circle, the coefficients are a = -2 and b = 4.
$$ O_2 = \left( - \frac{a}{2}, - \frac{b}{2} \right) = \left( - \frac{-2}{2}, - \frac{4}{2} \right) = (1, -2) $$
We use another formula to find the radii of the circles: \( r = \sqrt{ \left( - \frac{a}{2} \right)^2 + \left( - \frac{b}{2} \right)^2 - c } \).
For the first circle, a = -4, b = -8, c = 16:
$$ r_1 = \sqrt{ \left( - \frac{a}{2} \right)^2 + \left( - \frac{b}{2} \right)^2 - c } $$
$$ r_1 = \sqrt{ 2^2 + 4^2 - 16 } $$
$$ r_1 = \sqrt{ 4 + 16 - 16 } $$
$$ r_1 = \sqrt{ 4 } $$
$$ r_1 = 2 $$
For the second circle, a = -2, b = 4, c = -2:
$$ r_2 = \sqrt{ \left( - \frac{a}{2} \right)^2 + \left( - \frac{b}{2} \right)^2 - c } $$
$$ r_2 = \sqrt{ 1^2 + (-2)^2 - (-2) } $$
$$ r_2 = \sqrt{ 1 + 4 + 2 } $$
$$ r_2 = \sqrt{ 7 } $$
$$ r_2 \approx 2.65 $$
Next, I calculate the Euclidean distance between the centers of the two circles:
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
The center of the first circle is \( O_1 = (2, 4) \), so x1 = 2 and y1 = 4. The center of the second circle is \( O_2 = (1, -2) \), so x2 = 1 and y2 = -2.
$$ d = \sqrt{(1 - 2)^2 + (-2 - 4)^2} $$
$$ d = \sqrt{(-1)^2 + (-6)^2} $$
$$ d = \sqrt{1 + 36} $$
$$ d = \sqrt{37} \approx 6.08 $$
Then, I check if the condition for the circles being external is satisfied.
Two circles are external if the distance between their centers is greater than the sum of their radii:
$$ d > r_1 + r_2 $$
$$ 6.08 > 2 + 2.65 $$
$$ 6.08 > 4.65 $$
Since \( 6.08 > 4.65 \), we can conclude that the two circles are external and do not intersect or touch.
And so forth.
