Semicircumference

A semicircumference represents half of an entire circumference.

When you draw a diameter across a circle, it divides the circumference into two equal arcs, each one forming a semicircumference.

The length of a semicircumference is exactly half the total circumference of the circle.

$$ S_c = \pi \cdot r $$

Explanation. If r is the radius of the circle and the circumference is given by C = 2πr, then the length of a semicircumference is simply πr. $$ S_c = \frac{C}{2} = \frac{2 \pi \cdot r}{2} = \pi \cdot r $$

The region enclosed between the diameter and the semicircumference is called a semicircle.

The area of a semicircle is precisely half the area of the full circle.

$$ A_{sc} = \frac{r^2 \pi}{2} $$

Explanation. Since the area of a circle is A = πr², the area of a semicircle is calculated as follows: $$ A_{sc} = \frac{A}{2} = \frac{r^2 \pi}{2} $$

Remarks

Here are some key facts and observations about semicircumferences:

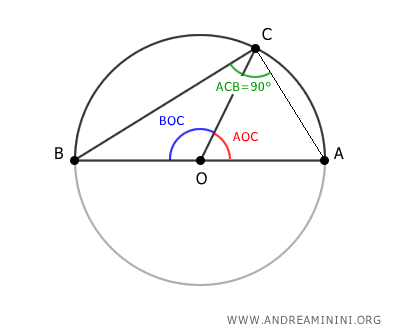
• Any angle inscribed in a semicircumference is a right angle
  This property is widely used in Euclidean geometry.

  Proof. Consider a circle with center O and a diameter AB.
  
  Pick any point C on the semicircumference between points A and B. We want to prove that angle ACB is a right angle (90°).
  
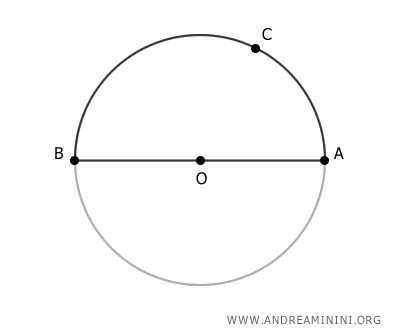
  Draw segment OC.
  
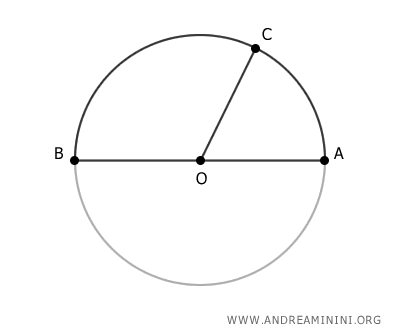
  Since OA and OB are both radii of the circle, they’re equal in length: OA ≅ OB. Likewise, OC is also a radius and is therefore equal in length to OA and OB. $$ \overline{OA} = \overline{OB} = \overline{OC} $$ The central angle AOC subtends arc AC, while angle BOC subtends arc BC. The central angle AOB, which spans the entire arc ACB, measures 180° because it extends across a semicircumference.
  
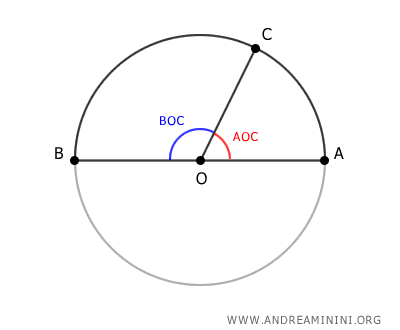
  The inscribed angle theorem states that an angle inscribed in a circle is equal to half the measure of the central angle that subtends the same arc. Therefore, if the central angle spanning arc ACB measures 180°, then the inscribed angle ACB is half of that, i.e. 90°. Hence, angle ACB is a right angle.
  

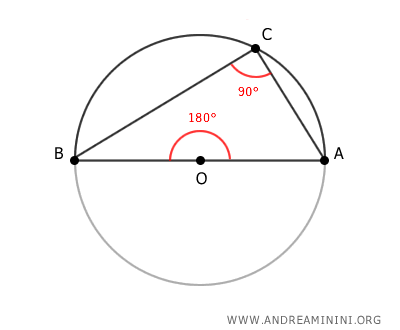
• Any triangle inscribed in a semicircumference is a right triangle, with the diameter serving as its hypotenuse
  This result also follows directly from the inscribed angle theorem. Since the central angle is 180°, the corresponding inscribed angle measures half of that, i.e. 90°.
  
  

And so on.